Gabarito
1/5 e 11/5
Não entendi, pois na resolução que tenho o cara pegou a inequação e desmembrou em duas assim depois igualou. Teria como fazer sem esse desmembramento?
Se sim como seria, se não. Gostaria do passo a passo.
Valeu amigos
ViniRFB




ViniRFB escreveu:(Esaf) Se -5 < 5x + 1 <5, então 1-x está entre:
ViniRFB escreveu:Não entendi, pois na resolução que tenho o cara pegou a inequação e desmembrou em duas assim depois igualou. Teria como fazer sem esse desmembramento?
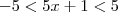

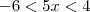
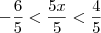
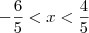
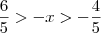
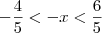
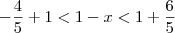
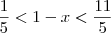

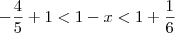

ViniRFB escreveu:Mas assim:
Como se resolve isso? Não tenho ideia de como saiu resultado.
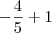 ?
?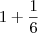 ?
?


Usuários navegando neste fórum: Nenhum usuário registrado e 5 visitantes


 , avisa que eu resolvo.
, avisa que eu resolvo.

