


silvia fillet escreveu:Divide-se um segmento de comprimento m em tres partes iguais e retira-se a parte central; para cada um dos 2 segmentos que 'sobram"repete-se o processo, retirando-se suas partes centrais e assim sucessivamente. Calcular a soma dos comprimentos retirados.
 .
.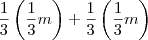 . Ou seja, retirou-se
. Ou seja, retirou-se  .
.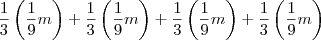 . Ou seja, retirou-se
. Ou seja, retirou-se  .
.


Rosana Vieira escreveu:Luiz Aquino eu cheguei nesta solução.
A1 = m e q = 2/3
PG
A1/1-q
S = m/1-2/3
S = m/1/3
S= 3m

Rosana Vieira escreveu:Luiz Aquino eu cheguei nesta solução.
A1 = m e q = 2/3
PG
A1/1-q
S = m/1-2/3
S = m/1/3
S= 3m

LuizAquino escreveu:Rosana Vieira escreveu:Luiz Aquino eu cheguei nesta solução.
A1 = m e q = 2/3
PG
A1/1-q
S = m/1-2/3
S = m/1/3
S= 3m
A sua solução não faz sentido.
Se temos um segmento de comprimento m e vamos retirar pedaços do mesmo, então como é que os pedaços retirados terão ao todo um tamanho maior do que m?
Veja a resolução de suas colegas.

Rosana Vieira escreveu:Então a resolução da Silvia está correta
 .
.

LuizAquino escreveu:Rosana Vieira escreveu:Então a resolução da Silvia está correta
Sim. Mas a resolução de vanessa_mat é mais adequada, pois ela usou que.

silvia fillet escreveu:Onde está a resoluçao da vanessamat?
Rosana Vieira escreveu:Luiz Aquino Gostaria de saber como vanessa_mat resolve neste exercício, pois não encontrei a sua resolução
vanessa_mat escreveu:Olá Rosana... acabei fazendo os mesmos cálculos, porém como quero saber a soma dos comprimentos retirados, considerei a1= m/3, r= 2/3 e na fórmula da P.G infinita acabou dando m.



Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.