 por Camila Z » Dom Fev 19, 2012 11:04
por Camila Z » Dom Fev 19, 2012 11:04
Oi, preciso de ajuda...
z^2-(2+i)z+2i=0
Obrigada
-
Camila Z
- Usuário Ativo

-
- Mensagens: 14
- Registrado em: Seg Jan 16, 2012 22:56
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Pedagogia
- Andamento: formado
 por fraol » Dom Fev 19, 2012 21:30
por fraol » Dom Fev 19, 2012 21:30
Boa noite,
Você pode resolver essa equação de várias formas, por exemplo:
1. Fatorando o polinômio ou
2. Aplicando a fórmula para resolução de equações de segundo grau, aquela famosa que aprendemos na educação básica ou
3. Aplicando as relações de Girard.
Para simplificar a resposta, vou usar a forma 3, ou seja as relações de Girard que tratam da soma e do produto das raízes, assim:
Sejam

e
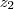
as raízes dessa equação,

( o fator de

),
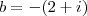
( o fator de

) e

( o termo independente ).
As relações de GIrard para a equação do 2o. grau são:
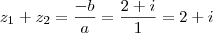
e

.
Viu como ficou simples, nesse caso. Ou seja estamos procurando 2 números complexos cuja Soma =

e cujo produto é
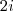
.
Agora é com você.
Isso ajuda?
-
fraol
- Colaborador Voluntário

-
- Mensagens: 392
- Registrado em: Dom Dez 11, 2011 20:08
- Localização: Mogi das Cruzes-SP
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: formado
 por Camila Z » Dom Fev 19, 2012 21:52
por Camila Z » Dom Fev 19, 2012 21:52
Mas se eu fizer com a forma básica de 2° grau, dá esses valores tb? Ainda não vi esses outros jeitos que vc falou, estou no início...
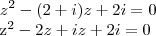
Não sei quem é a, b e c..., com certeza estou pensando errado...
-
Camila Z
- Usuário Ativo

-
- Mensagens: 14
- Registrado em: Seg Jan 16, 2012 22:56
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Pedagogia
- Andamento: formado
 por fraol » Dom Fev 19, 2012 22:12
por fraol » Dom Fev 19, 2012 22:12
Camila Z escreveu:Mas se eu fizer com a forma básica de 2° grau, dá esses valores tb?
Sim. Você pode usar a fórmula para resolução de equações do 2o. grau como eu disse na forma 2. Nesse caso será necessário extrair a raiz quadrada de um número complexo.
Ainda não vi esses outros jeitos que vc falou, estou no início...
O outro jeito citado é a fatoração que no caso da equação do 2o. grau consiste em reduzi-la a fatores envolvendo equações do 1o. grau. Basicamente é manipulação algébrica.
Não sei quem é a, b e c..., com certeza estou pensando errado...
Por favor, releia a minha ajuda, lá explicitei os valores de

,

e

.
-
fraol
- Colaborador Voluntário

-
- Mensagens: 392
- Registrado em: Dom Dez 11, 2011 20:08
- Localização: Mogi das Cruzes-SP
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: formado
 por Camila Z » Dom Fev 19, 2012 22:18
por Camila Z » Dom Fev 19, 2012 22:18
Então... ocorre que não sei fazer isso...

sim, eu vi os valores que vc colocou, mas me confundo para trabalhar com eles... calculo o delta e tudo?
-
Camila Z
- Usuário Ativo

-
- Mensagens: 14
- Registrado em: Seg Jan 16, 2012 22:56
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Pedagogia
- Andamento: formado
 por fraol » Dom Fev 19, 2012 22:41
por fraol » Dom Fev 19, 2012 22:41
Camila Z escreveu:Então... ocorre que não sei fazer isso...

sim, eu vi os valores que vc colocou, mas me confundo para trabalhar com eles... calculo o delta e tudo?
Sim.
-
fraol
- Colaborador Voluntário

-
- Mensagens: 392
- Registrado em: Dom Dez 11, 2011 20:08
- Localização: Mogi das Cruzes-SP
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: formado
 por Camila Z » Dom Fev 19, 2012 23:03
por Camila Z » Dom Fev 19, 2012 23:03
Ok, obrigada.
-
Camila Z
- Usuário Ativo

-
- Mensagens: 14
- Registrado em: Seg Jan 16, 2012 22:56
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Pedagogia
- Andamento: formado
Voltar para Números Complexos
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- equação irracional complexa
por viduani » Sex Jul 13, 2012 20:29
- 1 Respostas
- 2400 Exibições
- Última mensagem por fraol

Sex Jul 13, 2012 21:06
Álgebra Elementar
-
- funçao complexa
por timoteo » Qua Fev 13, 2013 14:22
- 3 Respostas
- 3323 Exibições
- Última mensagem por marinalcd

Ter Mar 05, 2013 13:28
Pedidos de Materiais
-
- Formula complexa - ajuda.
por mariosandes » Qui Out 21, 2010 11:24
- 2 Respostas
- 2412 Exibições
- Última mensagem por mariosandes

Sex Out 22, 2010 16:04
Matemática Financeira
-
- [Polinômio] com raiz complexa
por carolsiva » Qui Jan 09, 2014 09:45
- 3 Respostas
- 3768 Exibições
- Última mensagem por anderson_wallace

Qui Jan 09, 2014 23:24
Polinômios
-
- porcentagem questão complexa
por leandro moraes » Sáb Out 03, 2015 17:25
- 1 Respostas
- 5043 Exibições
- Última mensagem por nakagumahissao

Dom Out 04, 2015 12:17
Matemática Financeira
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



 e
e 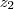 as raízes dessa equação,
as raízes dessa equação,  ( o fator de
( o fator de  ),
), 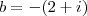 ( o fator de
( o fator de  ) e
) e  ( o termo independente ).
( o termo independente ).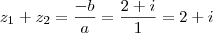 e
e  .
. e cujo produto é
e cujo produto é 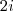 .
.
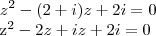

 ,
,  e
e  .
.









