 por Andrewo » Qui Fev 09, 2012 19:38
por Andrewo » Qui Fev 09, 2012 19:38
Aí galera tenho uns probleminhas aí que preciso tirar dúvidas,
O 1 e o 2 são pra transformar em 1 só radical
1) -
![\frac{\sqrt[4]{639}}{\sqrt[4]{71}} \frac{\sqrt[4]{639}}{\sqrt[4]{71}}](/latexrender/pictures/d90726f87ead628e2add285dd124fae7.png)

Onde eu cheguei :
![\sqrt[4]{\frac{9}{1}} \sqrt[4]{\frac{9}{1}}](/latexrender/pictures/91fa3b7c95b8983b3399c6f4a7729c85.png)
A resposta pelo gabarito:
![\sqrt[]{3} \sqrt[]{3}](/latexrender/pictures/b84ccc0f808c82dca2d7b0f887c64445.png)
2 -
![\sqrt[3]{\frac{y}{x}\sqrt[]{\frac{x}{y}}} \sqrt[3]{\frac{y}{x}\sqrt[]{\frac{x}{y}}}](/latexrender/pictures/959efb844a5d4bf8834afab8b8bfd59b.png)
Nesse eu tentei jogar o

pra dentro da raize ficaria
![\sqrt[3]{\sqrt[]{\frac{x}{y}}.{\frac{y}{x}}^{2}} \sqrt[3]{\sqrt[]{\frac{x}{y}}.{\frac{y}{x}}^{2}}](/latexrender/pictures/53c5226e39b1d419d0c2a68d8fb0d61f.png)
=
![\sqrt[6]{\frac{x}{y}}.{\frac{y}{x}}^{2} \sqrt[6]{\frac{x}{y}}.{\frac{y}{x}}^{2}](/latexrender/pictures/85ad30df93c58f5d132a647e18b085ed.png)
Resposta pelo gabarito:
![\sqrt[6]{\frac{y}{x}} \sqrt[6]{\frac{y}{x}}](/latexrender/pictures/de27f2612c26b7adb5a46838cb64a74f.png)
Esse aqui é p/ usar distributiva:
3-
![(\sqrt[]{5}-1) (\sqrt[]{5}+3) (\sqrt[]{5}-1) (\sqrt[]{5}+3)](/latexrender/pictures/3caf6c1bf9fdf4e5550652041c701b28.png)
O que eu fiz :
![5+3\sqrt[]{5}-\sqrt[]{5}-3 5+3\sqrt[]{5}-\sqrt[]{5}-3](/latexrender/pictures/74b003c940a1dd158011a4f59cb269a1.png)
=
![2+2\sqrt[]{5} 2+2\sqrt[]{5}](/latexrender/pictures/ca9769b2d64cec2575a6c2dce95302a6.png)
O resultado pelo gabarito é :
![2(1+\sqrt[]{5}) 2(1+\sqrt[]{5})](/latexrender/pictures/609a97f29d3b94adb3f510d98055faf0.png)
(será que tá errado esse gabarito????)
4-
![\frac{2}{\sqrt[]{2-\sqrt[]{3}}} \frac{2}{\sqrt[]{2-\sqrt[]{3}}}](/latexrender/pictures/cc7142bd63a79739d3826de42cf19de1.png)
Esse aqui é p/ racionalizar, mas não sei como fazer, tentei de varias maneiras.
Resposta :
![8+4\sqrt[]{3} 8+4\sqrt[]{3}](/latexrender/pictures/675bb85d97fcebe00b9426c7662f2275.png)
-

Andrewo
- Usuário Parceiro

-
- Mensagens: 54
- Registrado em: Qui Jan 12, 2012 11:22
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por MarceloFantini » Qui Fev 09, 2012 20:30
por MarceloFantini » Qui Fev 09, 2012 20:30
No primeiro você acertou, pois note que
![\sqrt[4]{\frac{9}{1}} = \frac{\sqrt[4]{9}}{1} = \frac{\sqrt[4]{3^2}}{1} = \frac{\sqrt[2]{3}}{1} = \sqrt{3} \sqrt[4]{\frac{9}{1}} = \frac{\sqrt[4]{9}}{1} = \frac{\sqrt[4]{3^2}}{1} = \frac{\sqrt[2]{3}}{1} = \sqrt{3}](/latexrender/pictures/14b818a4464063a16b96afc149a3c834.png)
.
No segundo, note
![\sqrt[3]{\frac{y}{x} \cdot \sqrt{\frac{x}{y}}} = \sqrt[3]{ \frac{y}{x} \cdot \frac{x^{ \frac{1}{2} } }{y^{ \frac{1}{2} } } } = \sqrt[3]{ \frac{y^{ \frac{1}{2} } }{x^{ \frac{1}{2} } } } = \sqrt[6]{ \frac{y}{x} } \sqrt[3]{\frac{y}{x} \cdot \sqrt{\frac{x}{y}}} = \sqrt[3]{ \frac{y}{x} \cdot \frac{x^{ \frac{1}{2} } }{y^{ \frac{1}{2} } } } = \sqrt[3]{ \frac{y^{ \frac{1}{2} } }{x^{ \frac{1}{2} } } } = \sqrt[6]{ \frac{y}{x} }](/latexrender/pictures/24629e6813288e2c45854a36ddcec950.png)
Sua resposta não está errada na terceira, você apenas não colocou em evidência:

.
Por último,
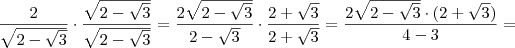
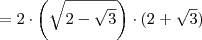
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Andrewo » Sex Fev 10, 2012 10:56
por Andrewo » Sex Fev 10, 2012 10:56
Vlw marcelo, ajudou mto, só to com duvidas nas 2 seguintes :
MarceloFantini escreveu:No segundo, note
![\sqrt[3]{\frac{y}{x} \cdot \sqrt{\frac{x}{y}}} = \sqrt[3]{ \frac{y}{x} \cdot \frac{x^{ \frac{1}{2} } }{y^{ \frac{1}{2} } } } = \sqrt[3]{ \frac{y^{ \frac{1}{2} } }{x^{ \frac{1}{2} } } } = \sqrt[6]{ \frac{y}{x} } \sqrt[3]{\frac{y}{x} \cdot \sqrt{\frac{x}{y}}} = \sqrt[3]{ \frac{y}{x} \cdot \frac{x^{ \frac{1}{2} } }{y^{ \frac{1}{2} } } } = \sqrt[3]{ \frac{y^{ \frac{1}{2} } }{x^{ \frac{1}{2} } } } = \sqrt[6]{ \frac{y}{x} }](/latexrender/pictures/24629e6813288e2c45854a36ddcec950.png)
Pq o
![\sqrt[3]{ \frac{y}{x} \cdot \frac{x^{ \frac{1}{2} } }{y^{ \frac{1}{2} } } } \sqrt[3]{ \frac{y}{x} \cdot \frac{x^{ \frac{1}{2} } }{y^{ \frac{1}{2} } } }](/latexrender/pictures/ce0e118f32be7ee8528a37e1bef832bd.png)
se transformou em
![\sqrt[3]{ \frac{y^{ \frac{1}{2} } }{x^{ \frac{1}{2} } } } \sqrt[3]{ \frac{y^{ \frac{1}{2} } }{x^{ \frac{1}{2} } } }](/latexrender/pictures/ebcf5487ca780111786fb82b2271c4fb.png)
Pois se isto é uma multiplicação de fração, então não seria :
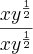
????
E tambem :
Por último,
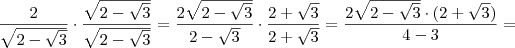
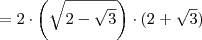
Eu tbm tentei fazer algo parecido, mas essa resposta que vc deu não bate com o gabarito
-

Andrewo
- Usuário Parceiro

-
- Mensagens: 54
- Registrado em: Qui Jan 12, 2012 11:22
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por MarceloFantini » Sex Fev 10, 2012 11:32
por MarceloFantini » Sex Fev 10, 2012 11:32
Você não percebeu que a fração é trocada, na primeira é

enquanto que na segunda é

. Assim, podemos reescrever como
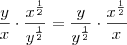
(estou trabalhando apenas com o que está dentro da raíz), e agora usando propriedades de expoentes como

e
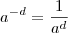
teremos que
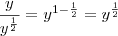
e

, daí
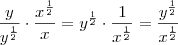
.
Sobre a outra, minha resposta está certa, a do gabarito não. Para verificar, coloque as duas expressões em
www.wolframalpha.com e verifique que numericamente elas são diferentes.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Radicais
por agfp5 » Sáb Out 30, 2010 08:50
- 2 Respostas
- 2330 Exibições
- Última mensagem por agfp5

Sáb Out 30, 2010 09:10
Geometria Plana
-
- Radicais
por Andrewo » Qua Fev 01, 2012 13:43
- 8 Respostas
- 4114 Exibições
- Última mensagem por LuizAquino

Qua Fev 08, 2012 12:22
Álgebra Elementar
-
- Radicais de nv
por Andrewo » Seg Fev 13, 2012 16:58
- 4 Respostas
- 2448 Exibições
- Última mensagem por Arkanus Darondra

Ter Fev 14, 2012 13:01
Álgebra Elementar
-
- Problema com radicais
por thadeu » Ter Nov 24, 2009 20:27
- 0 Respostas
- 1011 Exibições
- Última mensagem por thadeu

Ter Nov 24, 2009 20:27
Álgebra Elementar
-
- Limite com radicais
por valeuleo » Qui Mar 31, 2011 08:46
- 3 Respostas
- 5425 Exibições
- Última mensagem por LuizAquino

Qui Mar 31, 2011 11:41
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\frac{\sqrt[4]{639}}{\sqrt[4]{71}} \frac{\sqrt[4]{639}}{\sqrt[4]{71}}](/latexrender/pictures/d90726f87ead628e2add285dd124fae7.png)
 Onde eu cheguei :
Onde eu cheguei : ![\sqrt[4]{\frac{9}{1}} \sqrt[4]{\frac{9}{1}}](/latexrender/pictures/91fa3b7c95b8983b3399c6f4a7729c85.png)
![\sqrt[]{3} \sqrt[]{3}](/latexrender/pictures/b84ccc0f808c82dca2d7b0f887c64445.png)
![\sqrt[3]{\frac{y}{x}\sqrt[]{\frac{x}{y}}} \sqrt[3]{\frac{y}{x}\sqrt[]{\frac{x}{y}}}](/latexrender/pictures/959efb844a5d4bf8834afab8b8bfd59b.png)
 pra dentro da raize ficaria
pra dentro da raize ficaria ![\sqrt[3]{\sqrt[]{\frac{x}{y}}.{\frac{y}{x}}^{2}} \sqrt[3]{\sqrt[]{\frac{x}{y}}.{\frac{y}{x}}^{2}}](/latexrender/pictures/53c5226e39b1d419d0c2a68d8fb0d61f.png) =
=![\sqrt[6]{\frac{x}{y}}.{\frac{y}{x}}^{2} \sqrt[6]{\frac{x}{y}}.{\frac{y}{x}}^{2}](/latexrender/pictures/85ad30df93c58f5d132a647e18b085ed.png)
![\sqrt[6]{\frac{y}{x}} \sqrt[6]{\frac{y}{x}}](/latexrender/pictures/de27f2612c26b7adb5a46838cb64a74f.png)
![(\sqrt[]{5}-1) (\sqrt[]{5}+3) (\sqrt[]{5}-1) (\sqrt[]{5}+3)](/latexrender/pictures/3caf6c1bf9fdf4e5550652041c701b28.png)
![5+3\sqrt[]{5}-\sqrt[]{5}-3 5+3\sqrt[]{5}-\sqrt[]{5}-3](/latexrender/pictures/74b003c940a1dd158011a4f59cb269a1.png)
![2+2\sqrt[]{5} 2+2\sqrt[]{5}](/latexrender/pictures/ca9769b2d64cec2575a6c2dce95302a6.png)
![2(1+\sqrt[]{5}) 2(1+\sqrt[]{5})](/latexrender/pictures/609a97f29d3b94adb3f510d98055faf0.png) (será que tá errado esse gabarito????)
(será que tá errado esse gabarito????)![\frac{2}{\sqrt[]{2-\sqrt[]{3}}} \frac{2}{\sqrt[]{2-\sqrt[]{3}}}](/latexrender/pictures/cc7142bd63a79739d3826de42cf19de1.png)
![8+4\sqrt[]{3} 8+4\sqrt[]{3}](/latexrender/pictures/675bb85d97fcebe00b9426c7662f2275.png)


![\sqrt[4]{\frac{9}{1}} = \frac{\sqrt[4]{9}}{1} = \frac{\sqrt[4]{3^2}}{1} = \frac{\sqrt[2]{3}}{1} = \sqrt{3} \sqrt[4]{\frac{9}{1}} = \frac{\sqrt[4]{9}}{1} = \frac{\sqrt[4]{3^2}}{1} = \frac{\sqrt[2]{3}}{1} = \sqrt{3}](/latexrender/pictures/14b818a4464063a16b96afc149a3c834.png) .
.![\sqrt[3]{\frac{y}{x} \cdot \sqrt{\frac{x}{y}}} = \sqrt[3]{ \frac{y}{x} \cdot \frac{x^{ \frac{1}{2} } }{y^{ \frac{1}{2} } } } = \sqrt[3]{ \frac{y^{ \frac{1}{2} } }{x^{ \frac{1}{2} } } } = \sqrt[6]{ \frac{y}{x} } \sqrt[3]{\frac{y}{x} \cdot \sqrt{\frac{x}{y}}} = \sqrt[3]{ \frac{y}{x} \cdot \frac{x^{ \frac{1}{2} } }{y^{ \frac{1}{2} } } } = \sqrt[3]{ \frac{y^{ \frac{1}{2} } }{x^{ \frac{1}{2} } } } = \sqrt[6]{ \frac{y}{x} }](/latexrender/pictures/24629e6813288e2c45854a36ddcec950.png)
 .
.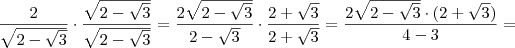
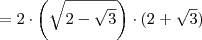


![\sqrt[3]{ \frac{y}{x} \cdot \frac{x^{ \frac{1}{2} } }{y^{ \frac{1}{2} } } } \sqrt[3]{ \frac{y}{x} \cdot \frac{x^{ \frac{1}{2} } }{y^{ \frac{1}{2} } } }](/latexrender/pictures/ce0e118f32be7ee8528a37e1bef832bd.png) se transformou em
se transformou em ![\sqrt[3]{ \frac{y^{ \frac{1}{2} } }{x^{ \frac{1}{2} } } } \sqrt[3]{ \frac{y^{ \frac{1}{2} } }{x^{ \frac{1}{2} } } }](/latexrender/pictures/ebcf5487ca780111786fb82b2271c4fb.png)
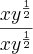 ????
???? . Assim, podemos reescrever como
. Assim, podemos reescrever como 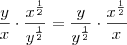 (estou trabalhando apenas com o que está dentro da raíz), e agora usando propriedades de expoentes como
(estou trabalhando apenas com o que está dentro da raíz), e agora usando propriedades de expoentes como  e
e 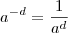 teremos que
teremos que 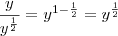 e
e  , daí
, daí 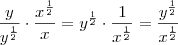 .
.