Exemplo:
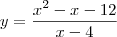
Li algures que o contradominio de uma função são todos os valores de y possíveis quando se substituí a variável independente por todos os valores possíveis para o dominio.
Analisando a função, posso concluír que não existem assintotas horizontais, e que a possível assintota vertical também não existe pois 4 anula tanto o denominador como o numerador. É precisamente em x=4 que existe um buraco no gráfico da função, diz-se que a função não está definida nesse ponto.
Simplificando:
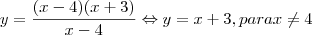
Posso concluír que o
 ?
?

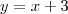 , logo
, logo  enquanto que o seu contradomínio (conjunto com os valores de y) será
enquanto que o seu contradomínio (conjunto com os valores de y) será 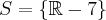 , ou você queria dizer que o seu domínio é esse ?? Pois em x=7 não existe indeterminação da função.
, ou você queria dizer que o seu domínio é esse ?? Pois em x=7 não existe indeterminação da função.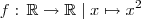 . Note que a função nunca retornará um valor negativo, entretanto a priori ela pode. Então o contradomínio pode ser os reais, mas a imagem será
. Note que a função nunca retornará um valor negativo, entretanto a priori ela pode. Então o contradomínio pode ser os reais, mas a imagem será 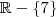 na sua questão.
na sua questão.



 .
.



