Gostaria que alguém me ajuda a resolver este exercício.
1. Considere o triângulo ABC, isósceles com base BC, onde os segmentos de reta BC, CD, DE, EF e FA são congruentes. Determine as medidas dos ângulos do triângulo ABC.
2. Um pedaço de papel cartão tem a forma de um triângulo isósceles, de altura igual a 12 cm. Foi dividido por uma reta paralela à base do triângulo, em dois pedaços de mesma área. Determine a altura da parte triangular obtida na secção.
Não conseguir colar os desenhos



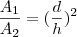
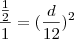









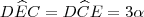

 º
º º
º
 , avisa que eu resolvo.
, avisa que eu resolvo.

