 por Rosana Vieira » Sáb Fev 04, 2012 13:23
por Rosana Vieira » Sáb Fev 04, 2012 13:23
Gostaria que alguém me ajuda a resolver este exercício.
1. Considere o triângulo ABC, isósceles com base BC, onde os segmentos de reta BC, CD, DE, EF e FA são congruentes. Determine as medidas dos ângulos do triângulo ABC.
2. Um pedaço de papel cartão tem a forma de um triângulo isósceles, de altura igual a 12 cm. Foi dividido por uma reta paralela à base do triângulo, em dois pedaços de mesma área. Determine a altura da parte triangular obtida na secção.
Não conseguir colar os desenhos
-
Rosana Vieira
- Usuário Parceiro

-
- Mensagens: 74
- Registrado em: Qui Nov 17, 2011 00:11
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por Arkanus Darondra » Sáb Fev 04, 2012 18:59
por Arkanus Darondra » Sáb Fev 04, 2012 18:59
Rosana Vieira escreveu:Não conseguir colar os desenhos
Você pode hospedar sua imagem no site:
http://imageshack.us/Para isso, após criar e logar na sua conta, clique em browse e selecione sua imagem.
Você será redirecionada para outra página. No canto esquerdo você verá "Direct Link". Copie.
Volte ao fórum, pressione o botão "Img" que você vê acima de onde digita a mensagem e cole o link.
Para conferir, clique em "Prever".
Rosana Vieira escreveu:2. Um pedaço de papel cartão tem a forma de um triângulo isósceles, de altura igual a 12 cm. Foi dividido por uma reta paralela à base do triângulo, em dois pedaços de mesma área. Determine a altura da parte triangular obtida na secção.

Por razão de semelhança temos e considerando que, como as duas áreas são iguais, cada uma divide a área total ao meio:
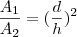
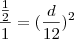



-
Arkanus Darondra
- Colaborador Voluntário

-
- Mensagens: 187
- Registrado em: Seg Dez 26, 2011 18:19
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Cesar » Sáb Fev 04, 2012 20:34
por Cesar » Sáb Fev 04, 2012 20:34
Rosana Vieira escreveu:Gostaria que alguém me ajuda a resolver este exercício.
1. Considere o triângulo ABC, isósceles com base BC, onde os segmentos de reta BC, CD, DE, EF e FA são congruentes. Determine as medidas dos ângulos do triângulo ABC.
2. Um pedaço de papel cartão tem a forma de um triângulo isósceles, de altura igual a 12 cm. Foi dividido por uma reta paralela à base do triângulo, em dois pedaços de mesma área. Determine a altura da parte triangular obtida na secção.
Não conseguir colar os desenhos
amigo tudo bem?
gostaria de perguntar o seguinte, porque o lado direito esta elevado ao quadrado?
desculpe se estiver perguntando algo obvio
cesar
-
Cesar
- Usuário Dedicado

-
- Mensagens: 29
- Registrado em: Sex Out 21, 2011 23:10
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Matematica
- Andamento: cursando
 por Arkanus Darondra » Sáb Fev 04, 2012 21:11
por Arkanus Darondra » Sáb Fev 04, 2012 21:11
Cesar escreveu:amigo tudo bem?
gostaria de perguntar o seguinte, porque o lado direito esta elevado ao quadrado?
desculpe se estiver perguntando algo obvio
cesar
Olá Cesar. Tudo bem.
Recomendo que você dê uma olhada neste site:
http://www.cienciamao.usp.br/dados/t2k/ ... rquivo.pdf 
-
Arkanus Darondra
- Colaborador Voluntário

-
- Mensagens: 187
- Registrado em: Seg Dez 26, 2011 18:19
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Arkanus Darondra » Sáb Fev 04, 2012 22:07
por Arkanus Darondra » Sáb Fev 04, 2012 22:07
Rosana, acabo de ver uma pergunta igual a sua no fórum. Segue a resolução:

Se
 Propriedade:
Propriedade: "
a medida de um ângulo externo é igual à soma das medidas dos 2 ângulos internos não adjacentes"
Então de acordo com os dados do enunciado e com a propriedade:

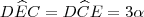

Logo:

º

º

-
Arkanus Darondra
- Colaborador Voluntário

-
- Mensagens: 187
- Registrado em: Seg Dez 26, 2011 18:19
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
Voltar para Geometria Plana
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Geometria Plana
por claudia » Qui Out 23, 2008 16:11
- 1 Respostas
- 8719 Exibições
- Última mensagem por admin

Ter Out 28, 2008 16:47
Geometria Plana
-
- Geometria plana
por Rayanne07 » Qua Jan 13, 2010 17:40
- 3 Respostas
- 4704 Exibições
- Última mensagem por Rayanne07

Sex Jan 15, 2010 10:46
Geometria Plana
-
- Geometria Plana
 por MelvinMyster » Sex Ago 13, 2010 10:07
por MelvinMyster » Sex Ago 13, 2010 10:07
- 1 Respostas
- 4820 Exibições
- Última mensagem por alexandre32100

Sex Ago 13, 2010 13:15
Geometria Plana
-
- Geometria plana
 por Paulo A G » Qua Jan 26, 2011 16:11
por Paulo A G » Qua Jan 26, 2011 16:11
- 0 Respostas
- 2538 Exibições
- Última mensagem por Paulo A G

Qua Jan 26, 2011 16:11
Geometria Plana
-
- geometria plana
 por Abner » Seg Jan 31, 2011 17:53
por Abner » Seg Jan 31, 2011 17:53
- 3 Respostas
- 3673 Exibições
- Última mensagem por Abner

Ter Fev 01, 2011 17:31
Geometria Plana
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



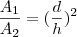
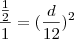









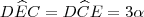

 º
º º
º

 substitui-se
substitui-se 
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.