Alguém pode me ajudar?
Sejam T, S operadores lineares de V em V, (V é espaço vetorial). Mostre que se (S o T - I) é injetora entõ (T o S - I) é injetora , (I é a identidade).
(Sugestão: SoT(ToS-I) = (SoT-I)oS.)



nietzsche escreveu:Sejam T, S operadores lineares de V em V, (V é espaço vetorial). Mostre que se (S o T - I) é injetora entõ (T o S - I) é injetora , (I é a identidade).
(Sugestão: SoT(ToS-I) = (SoT-I)oS.)
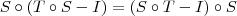 .
.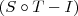 é injetora. Como sabemos que I é injetora, temos que S será injetora (justifique essa passagem).
é injetora. Como sabemos que I é injetora, temos que S será injetora (justifique essa passagem).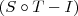 e S são injetoras, temos que
e S são injetoras, temos que  é injetora (justifique essa passagem).
é injetora (justifique essa passagem).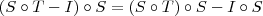
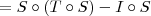
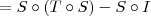
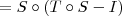

 é injetora, temos que
é injetora, temos que 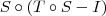 também é injetora.
também é injetora.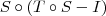 e S são injetoras, temos que
e S são injetoras, temos que 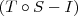 é injetora (justifique essa passagem).
é injetora (justifique essa passagem).

nietzsche escreveu:Você disse:
"Por hipótese, (SoT - I) é injetora. Como sabemos que I é injetora, temos que S será injetora (justifique essa passagem)"
mas como provo que S é injetora?
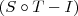 caso S não fosse injetora.
caso S não fosse injetora.nietzsche escreveu:Acho que o certo é:
Se T é um operador,
ToU = I => T é sobrejetora (no problema não seria S é sobrejtora pois tem inversa a direta?)
SoT = I => T é injetora


nietzsche escreveu:Mas nesse problema a dimensão do espaço vetorial V não é finita, logo não posso usar o teorema do núcleo/imagem nem dizer que se T é sobrejetiva, então é injetiva.



nietzsche escreveu:Se quiser tentar resolver, seria bom, mas acabei resolvendo.

 Nuc(ToS-I) => v=0.
Nuc(ToS-I) => v=0. Nuc(ToS-I), temos pela definição de núcleo que (ToS-I)(v) = 0. (*)
Nuc(ToS-I), temos pela definição de núcleo que (ToS-I)(v) = 0. (*)
nietzsche escreveu:Queremos provar que:
Para todo vNuc(ToS-I) => v=0.
Para todo vNuc(ToS-I), temos pela definição de núcleo que (ToS-I)(v) = 0. (*)
Aplicando S dos dois lados e usando que S é uma transformação linear: S(ToS-I)(v) = S(0) = 0.
Usando a dica, temos que: (SoT-I)oS(v)=0.
Por hipótese, se SoT-I é injetiva, então Nuc(SoT) = {0}.
Portanto, Sv=0.
Usando que Sv=0 em (*): (ToS-I)(v) = (ToS)(v) -Iv = T(S(v)) - v = T(0)- v =0.
Usando que T é linear: v = T(0) = 0.
Portanto, v=0.
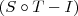 é injetora. Como sabemos que I é injetora, temos que S será injetora.
é injetora. Como sabemos que I é injetora, temos que S será injetora.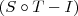 é injetora mesmo sendo S não injetora.
é injetora mesmo sendo S não injetora.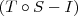 é injetora.
é injetora.

Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes

 .
.
 :
: