Espero que possam me ajudar estou com dúvida em uma questão onde se pede para determinar o subespaço gerado pelos vetores de um conjunto dado, a questão tem vária letras mas a que me causou duvidas foi a seguinte:
Então eu montei uma equação na qual uma matriz generica 2x2 sera igual a soma dos vetores(v1,v2,v3) multiplicados pelos escalares com os escalares(a,b,c) , com isso chego em um sistema de 4 equações e 3 icógnitas (a,b,c). Só que eu chego no seguinte ponto do sistema e tenho duvida no que fazer:
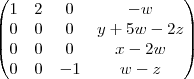
Até pensei em deixar x,y e z em função de w e z e o espaço vetorial seria esse:
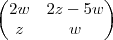
Porém a resposta é essa:
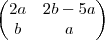
Isso que não entendi, é só chamar w de a e z de b que fica certo,queria saber o que estou errando. Quem souber me ajude pois tenho prova de álgebra linear quinta agora, pois como a faculdade ficou de greve tive apenas 2 semanas de férias. Caso tenha postado no lugar errado me desculpem, sou novo no fórum.
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png "\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}")
![\sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png "\sqrt[]{2}")
e elevar ao quadrado os dois lados)