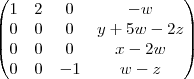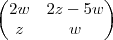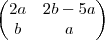por cotonete » Dom Jan 22, 2012 23:34
por cotonete » Dom Jan 22, 2012 23:34
Olá,
Espero que possam me ajudar estou com dúvida em uma questão onde se pede para determinar o subespaço gerado pelos vetores de um conjunto dado, a questão tem vária letras mas a que me causou duvidas foi a seguinte:

Então eu montei uma equação na qual uma matriz generica 2x2 sera igual a soma dos vetores(v1,v2,v3) multiplicados pelos escalares com os escalares(a,b,c) , com isso chego em um sistema de 4 equações e 3 icógnitas (a,b,c). Só que eu chego no seguinte ponto do sistema e tenho duvida no que fazer:
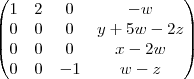
Até pensei em deixar x,y e z em função de w e z e o espaço vetorial seria esse:
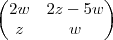
Porém a resposta é essa:
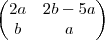
Isso que não entendi, é só chamar w de a e z de b que fica certo,queria saber o que estou errando. Quem souber me ajude pois tenho prova de álgebra linear quinta agora, pois como a faculdade ficou de greve tive apenas 2 semanas de férias. Caso tenha postado no lugar errado me desculpem, sou novo no fórum.
-
cotonete
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Dom Jan 22, 2012 22:52
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Metalúrgica
- Andamento: cursando
 por MarceloFantini » Seg Jan 23, 2012 05:52
por MarceloFantini » Seg Jan 23, 2012 05:52
Mas a letra não faz diferença, sua resposta está certa.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por cotonete » Seg Jan 23, 2012 21:50
por cotonete » Seg Jan 23, 2012 21:50
E eu me matando igual um doido por causa dessas letras,muito obrigado MarceloFantini, pode parecer uma dúvida besta mas eu realmente não estava seguro com aquela respoosta, mas agora percebi que estou pelo caminho certo.
-
cotonete
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Dom Jan 22, 2012 22:52
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Metalúrgica
- Andamento: cursando
Voltar para Matrizes e Determinantes
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Combinação Linear das Matrizes
por Jamilly » Qua Mar 17, 2010 22:51
- 4 Respostas
- 16978 Exibições
- Última mensagem por Jamilly

Qua Mar 24, 2010 21:06
Álgebra Linear
-
- combinaçao linear
por carolms » Dom Jun 15, 2008 20:59
- 1 Respostas
- 6320 Exibições
- Última mensagem por admin

Seg Jun 16, 2008 13:56
Geometria Analítica
-
- Combinação linear
por Armat » Qua Fev 04, 2009 18:12
- 0 Respostas
- 5461 Exibições
- Última mensagem por Armat

Qua Fev 04, 2009 18:12
Geometria Analítica
-
- Combinação Linear
por -civil- » Sáb Mai 07, 2011 11:28
- 1 Respostas
- 2100 Exibições
- Última mensagem por LuizAquino

Sáb Mai 07, 2011 11:44
Geometria Espacial
-
- Combinação Linear
por -civil- » Sáb Mai 07, 2011 11:33
- 2 Respostas
- 2256 Exibições
- Última mensagem por -civil-

Sáb Mai 07, 2011 22:21
Geometria Espacial
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.