Valeww fraol pela resposta; Então deixa eu ver se eu entendi direito, você está supondo que se
b for divisor de
a implica que
a é multiplo de
b, que legal , mais eu observei uma coisa que
a é maior que
b, se você analizar a sequência. Porem quanto mais mais o conjunto
b vai crescendo eu podi observar que vai englobando o conjunto
a, parabens pela sua percepção , eu vi essa questão e analizei da forma errada , eu analizei que se
b for divisor de
a implicaria que
b teria que ser maior do que correto? mais mesmo assim obrigado de novo, eu vou estudar esse livro de matemática "Matemática - Aula por Aula" , alias essa pergunda é desse livro que eu mencionei. Você poderia Passar um livro que seja bom para eu estudar, nem que seje americano (pois o livros de matemáticas americanos são bons), ou um artigo mais eu prefiro livro mesmo se não for encomodo para eu melhorar a minha lógica de pensar.....


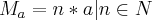 e
e  , Com a e b naturais não nulos então
, Com a e b naturais não nulos então  é subconjunto de
é subconjunto de 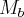 sempre que:
sempre que:




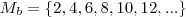
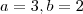
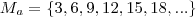
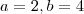
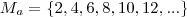

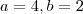
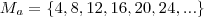
 será um conjunto contendo múltiplos b
será um conjunto contendo múltiplos b 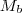 será o conjunto de todos os múltiplos de b e portanto
será o conjunto de todos os múltiplos de b e portanto 




 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.