Numa função trigonométrica, podemos desde logo identificar: amplitude, periodo e deslocamentos horizontal e vertical.
Amplitude: 3
Periodo:
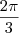
Deslocamento horizontal: -1 (para a esquerda)
Deslocamento vertical: 3 (para cima)
Agora divide o periodo em 4 partes:

Agora ao ponto -1 soma 4 vezes o resultado anterior.De cada vez que somares anota o resultado.Será útil colocares tudo com o mesmo denominador.
Por fim substitui
x na função pelos valores obtidos.Se tudo correu bem, vai obter 1, 0 ,-1,0 e 1.Marca as coordenadas, acabaste de esboçar um periodo da função.
Esta questão esta relacionada com as transformações de funções trigonometricas.
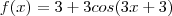 ?
?
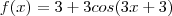 ?
?
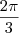


 temos que:
temos que: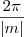
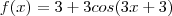 ,
,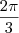 e o deslocamento vertical ser ser 3.
e o deslocamento vertical ser ser 3.

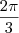 para
para 

