 por matem » Ter Nov 29, 2011 17:03
por matem » Ter Nov 29, 2011 17:03
Sabendo que os números x, x+9,e x+45, formam nessa ordem uma pg de termos não nulos determine x e escreva a pg.
-
matem
- Usuário Dedicado

-
- Mensagens: 31
- Registrado em: Seg Nov 28, 2011 18:04
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
 por MarceloFantini » Ter Nov 29, 2011 19:11
por MarceloFantini » Ter Nov 29, 2011 19:11
Você tentou usar as propriedades de progressão geométrica?
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por matem » Ter Nov 29, 2011 20:42
por matem » Ter Nov 29, 2011 20:42
MarceloFantini escreveu:Você tentou usar as propriedades de progressão geométrica?
SIM, MAS ENCONTREI A RAZÃO 3 DEPOIS 9 E ESTOU INSEGURA DE RESPONDER POIS VALE NOTA ESTE TRABALHO
-
matem
- Usuário Dedicado

-
- Mensagens: 31
- Registrado em: Seg Nov 28, 2011 18:04
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
 por MarceloFantini » Ter Nov 29, 2011 20:46
por MarceloFantini » Ter Nov 29, 2011 20:46
Use a propriedade que

. A resposta sairá facilmente.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por matem » Ter Nov 29, 2011 20:52
por matem » Ter Nov 29, 2011 20:52
MarceloFantini escreveu:Use a propriedade que

. A resposta sairá facilmente.
VOU MOSTRAR COMO FIZ:A2/A1=A3/A2 =X+9/X=X+45/X+9
(X+9)²=X²+18X+81
X²=81
X=9
ENCONTREI 9,18,54
-9,0,-36
NÃO TENHO CERTEZA DE ESTAR CORRETO
-
matem
- Usuário Dedicado

-
- Mensagens: 31
- Registrado em: Seg Nov 28, 2011 18:04
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
 por MarceloFantini » Ter Nov 29, 2011 20:56
por MarceloFantini » Ter Nov 29, 2011 20:56
O que você fez está errado, reveja minha mensagem anterior. A conta correta é

, que é a resposta correta da multiplicação em cruz das frações.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por matem » Ter Nov 29, 2011 21:27
por matem » Ter Nov 29, 2011 21:27
MarceloFantini escreveu:O que você fez está errado, reveja minha mensagem anterior. A conta correta é

, que é a resposta correta da multiplicação em cruz das frações.
POR FAVOR ME EXPLIQUE
X²+18X+81
X²=9
X=3
3,12,48
-3,6,41?
-
matem
- Usuário Dedicado

-
- Mensagens: 31
- Registrado em: Seg Nov 28, 2011 18:04
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
 por matem » Ter Nov 29, 2011 21:34
por matem » Ter Nov 29, 2011 21:34
matem escreveu:MarceloFantini escreveu:O que você fez está errado, reveja minha mensagem anterior. A conta correta é

, que é a resposta correta da multiplicação em cruz das frações.
POR FAVOR ME EXPLIQUE
X²+18X+81
X²=9
X=3
3,12,48
-3,6,41?
X²+18X+81=X²+45X
X²-X²+18X-45X+81=0
27X+81=0????
-
matem
- Usuário Dedicado

-
- Mensagens: 31
- Registrado em: Seg Nov 28, 2011 18:04
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
 por MarceloFantini » Qua Nov 30, 2011 00:18
por MarceloFantini » Qua Nov 30, 2011 00:18
Faltou um sinal, é
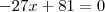
, daí

.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por DanielFerreira » Sáb Jan 07, 2012 20:35
por DanielFerreira » Sáb Jan 07, 2012 20:35
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
Voltar para Progressões
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Progressao] série geometrica X progressao geometrica?
por aajunim » Seg Mar 18, 2013 11:19
- 2 Respostas
- 4254 Exibições
- Última mensagem por aajunim

Ter Mar 19, 2013 11:44
Progressões
-
- Progressão aritmética e progressão geométrica
por Danilo Dias Vilela » Sex Mar 12, 2010 13:41
- 1 Respostas
- 4726 Exibições
- Última mensagem por thadeu

Sex Mar 12, 2010 17:36
Progressões
-
- Progressão geométrica (ITA)
por Ananda » Sex Mar 07, 2008 13:27
- 17 Respostas
- 25553 Exibições
- Última mensagem por Ananda

Qui Mar 13, 2008 11:10
Progressões
-
- Progressão Geométrica
por nicecaps » Seg Mar 22, 2010 11:37
- 2 Respostas
- 4238 Exibições
- Última mensagem por nicecaps

Ter Mar 23, 2010 09:45
Progressões
-
- Progressão Geométrica
por Jessie » Qui Abr 29, 2010 17:49
- 1 Respostas
- 2891 Exibições
- Última mensagem por Elcioschin

Qui Abr 29, 2010 20:12
Pedidos
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.







. A resposta sairá facilmente.

 , que é a resposta correta da multiplicação em cruz das frações.
, que é a resposta correta da multiplicação em cruz das frações.

, que é a resposta correta da multiplicação em cruz das frações.

, que é a resposta correta da multiplicação em cruz das frações.


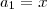
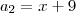
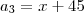
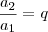

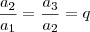

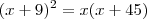


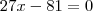

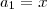 =============> 3
=============> 3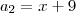 ==========> 3 + 9 = 12
==========> 3 + 9 = 12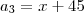 =========> 3 + 45 = 48
=========> 3 + 45 = 48
 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
