 por TiagoFERD » Dom Dez 25, 2011 08:05
por TiagoFERD » Dom Dez 25, 2011 08:05
Bom dia! sou novo por aqui.
Espero que alguem me ajude em uma dúvida sobre subespaço vectorial.
Na solução do livro diz que não é um Subespaço Vectorial, mas eu verifiquei e a mim deu um subespaço.
Aqui está a imagem.
Muito Obrigado.
-
TiagoFERD
- Usuário Ativo

-
- Mensagens: 24
- Registrado em: Dom Out 23, 2011 04:49
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
 por fraol » Dom Dez 25, 2011 10:59
por fraol » Dom Dez 25, 2011 10:59
Oi TIago,
No teste 1 você está certo, pois
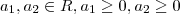
então

.
No teste 2 não, pois
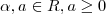
então

nem sempre é maior do que ou igual a 0. Por quê?
Bom natal,
Francisco.
-
fraol
- Colaborador Voluntário

-
- Mensagens: 392
- Registrado em: Dom Dez 11, 2011 20:08
- Localização: Mogi das Cruzes-SP
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: formado
 por TiagoFERD » Seg Dez 26, 2011 13:09
por TiagoFERD » Seg Dez 26, 2011 13:09
fraol escreveu:Oi TIago,
No teste 1 você está certo, pois
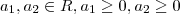
então

.
No teste 2 não, pois
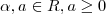
então

nem sempre é maior do que ou igual a 0. Por quê?
Bom natal,
Francisco.
Boas Francisco muito Obrigado e bom Natal para você também.
bem será porque o resposta é porque ou será zero ou maior do que zero?
não sei se entendi...
Obrigado
-
TiagoFERD
- Usuário Ativo

-
- Mensagens: 24
- Registrado em: Dom Out 23, 2011 04:49
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
 por fraol » Seg Dez 26, 2011 14:29
por fraol » Seg Dez 26, 2011 14:29
Olá Tiago,
Para ser um subespaço vetorial é necessário que se preserve a soma dos vetores e a multiplicação por escalar. Isto é:
1) A soma de 2 vetores quaisquer do subespaço deve dar um vetor também pertencente ao subespaço.
Isso nós vimos que sempre acontece pois como a única restrição é o
a >= 0 então sempre que somarmos dois vetores vamos obter um terceiro cujo
a correspondente será sempre >= 0.
2) A multiplicação de um vetor qualquer do subespaço por um número real (alfa) deve dar um vetor também pertencente ao subespaço.
Neste caso, se tomamos um alfa negativo, então o
a correspondente do novo vetor será negativo e aí não satisfaz a restrição do subespaço. Ou seja

é negativo se o

.
Se não tiver entendido manda de volta que a gente vai conversando...
Até mais,
Francisco.
-
fraol
- Colaborador Voluntário

-
- Mensagens: 392
- Registrado em: Dom Dez 11, 2011 20:08
- Localização: Mogi das Cruzes-SP
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: formado
 por TiagoFERD » Seg Dez 26, 2011 14:34
por TiagoFERD » Seg Dez 26, 2011 14:34
fraol escreveu:Olá Tiago,
Para ser um subespaço vetorial é necessário que se preserve a soma dos vetores e a multiplicação por escalar. Isto é:
1) A soma de 2 vetores quaisquer do subespaço deve dar um vetor também pertencente ao subespaço.
Isso nós vimos que sempre acontece pois como a única restrição é o
a >= 0 então sempre que somarmos dois vetores vamos obter um terceiro cujo
a correspondente será sempre >= 0.
2) A multiplicação de um vetor qualquer do subespaço por um número real (alfa) deve dar um vetor também pertencente ao subespaço.
Neste caso, se tomamos um alfa negativo, então o
a correspondente do novo vetor será negativo e aí não satisfaz a restrição do subespaço. Ou seja

é negativo se o

.
Se não tiver entendido manda de volta que a gente vai conversando...
Até mais,
Francisco.
Boas fraol, não tinha pensado no caso do alfa menor que 0! que cabeça!! :( muito obrigado.
bom natal
-
TiagoFERD
- Usuário Ativo

-
- Mensagens: 24
- Registrado em: Dom Out 23, 2011 04:49
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Subespaço Vetorial] Subespaço envolvendo matrizes
por hyge » Qua Mai 02, 2018 17:04
- 2 Respostas
- 10991 Exibições
- Última mensagem por adauto martins

Dom Mai 06, 2018 12:28
Álgebra Linear
-
- [Subespaço Vetorial] Verificar que é o conjunto é subespaço
por anderson_wallace » Seg Dez 30, 2013 17:56
- 3 Respostas
- 4687 Exibições
- Última mensagem por Renato_RJ

Ter Dez 31, 2013 14:00
Álgebra Linear
-
- subespaço
por alzenir agapito » Qui Jul 21, 2011 17:52
- 0 Respostas
- 1780 Exibições
- Última mensagem por alzenir agapito

Qui Jul 21, 2011 17:52
Álgebra
-
- subespaço vetorial
 por leobcastro » Seg Jun 16, 2008 10:18
por leobcastro » Seg Jun 16, 2008 10:18
- 8 Respostas
- 26984 Exibições
- Última mensagem por Heidji

Qua Jan 27, 2010 23:16
Geometria Analítica
-
- Exercício de subespaço
por ClaudianeLoira » Qua Jun 18, 2008 00:29
- 1 Respostas
- 1848 Exibições
- Última mensagem por admin

Qua Jun 18, 2008 03:22
Tópicos sem Interação (leia as regras)
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



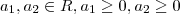 então
então  .
.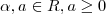 então
então  nem sempre é maior do que ou igual a 0. Por quê?
nem sempre é maior do que ou igual a 0. Por quê?
então
.
então
nem sempre é maior do que ou igual a 0. Por quê?

 é negativo se o
é negativo se o  .
.
é negativo se o
.



 substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.