Bom dia! sou novo por aqui.
Espero que alguem me ajude em uma dúvida sobre subespaço vectorial.
Na solução do livro diz que não é um Subespaço Vectorial, mas eu verifiquei e a mim deu um subespaço.
Aqui está a imagem.
Muito Obrigado.



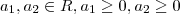 então
então  .
.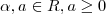 então
então  nem sempre é maior do que ou igual a 0. Por quê?
nem sempre é maior do que ou igual a 0. Por quê?
fraol escreveu:Oi TIago,
No teste 1 você está certo, poisentão
.
No teste 2 não, poisentão
nem sempre é maior do que ou igual a 0. Por quê?
Bom natal,
Francisco.

 é negativo se o
é negativo se o  .
.
fraol escreveu:Olá Tiago,
Para ser um subespaço vetorial é necessário que se preserve a soma dos vetores e a multiplicação por escalar. Isto é:
1) A soma de 2 vetores quaisquer do subespaço deve dar um vetor também pertencente ao subespaço.
Isso nós vimos que sempre acontece pois como a única restrição é o a >= 0 então sempre que somarmos dois vetores vamos obter um terceiro cujo a correspondente será sempre >= 0.
2) A multiplicação de um vetor qualquer do subespaço por um número real (alfa) deve dar um vetor também pertencente ao subespaço.
Neste caso, se tomamos um alfa negativo, então o a correspondente do novo vetor será negativo e aí não satisfaz a restrição do subespaço. Ou sejaé negativo se o
.
Se não tiver entendido manda de volta que a gente vai conversando...
Até mais,
Francisco.

Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
