 por Richard Oliveira » Seg Dez 19, 2011 17:31
por Richard Oliveira » Seg Dez 19, 2011 17:31
Olá, estou estudando funções e não consegui entender a resolução dessa questão:

Resolução:
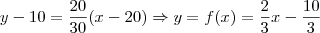
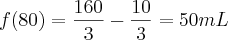
Cada aplicação =
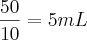
Não entendi como foi resolvida a questão, se puderem me responder agradeço.
"Eu editei o post porque eu havia errado a resolução".
-
Richard Oliveira
- Usuário Ativo

-
- Mensagens: 20
- Registrado em: Sex Nov 04, 2011 16:07
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por MarceloFantini » Seg Dez 19, 2011 19:17
por MarceloFantini » Seg Dez 19, 2011 19:17
Qual foi sua maior dificuldade? Que ponto em especial você não entendeu?
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Richard Oliveira » Seg Dez 19, 2011 22:21
por Richard Oliveira » Seg Dez 19, 2011 22:21
Esqueci de dizer o meu problema. Eu não entendi de onde surgiu essa equação:

É alguma propriedade que eu não sei? alguma regra?
-
Richard Oliveira
- Usuário Ativo

-
- Mensagens: 20
- Registrado em: Sex Nov 04, 2011 16:07
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por MarceloFantini » Seg Dez 19, 2011 23:07
por MarceloFantini » Seg Dez 19, 2011 23:07
Isto é apenas a aplicação da equação de uma reta que passa pro um ponto
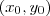
e tem coeficiente angular

, veja:
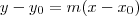
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por MarceloFantini » Ter Dez 20, 2011 23:50
por MarceloFantini » Ter Dez 20, 2011 23:50
Foram tirados do gráfico. Veja que os pontos
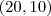
e
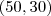
pertencem ao gráfico, ele escolheu o primeiro como
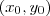
de referência, e o coeficiente angular é dado por
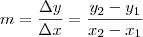
. Escolhendo os pontos dados, temos:
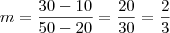
.
Recomendo fortemente que reestude geometria analítica, estes são conceitos fundamentais e iniciais.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Richard Oliveira » Qua Dez 21, 2011 01:30
por Richard Oliveira » Qua Dez 21, 2011 01:30
Ah sim, entendi, não tinha entendido como havia sido tirado do gráfico. Bem explicado. Agradeço por ajudar e também pela recomendação do tema a ser estudado, pois o que eu preciso é disso mesmo, se for se apegar nesses exercícios sem saber o "caminho que estou percorrendo" vai ser difícil. Obrigado.
-
Richard Oliveira
- Usuário Ativo

-
- Mensagens: 20
- Registrado em: Sex Nov 04, 2011 16:07
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Funções reais. como resolver estas funções...
por LEANDRO HENRIQUE » Ter Mar 04, 2014 18:43
- 0 Respostas
- 3429 Exibições
- Última mensagem por LEANDRO HENRIQUE

Ter Mar 04, 2014 18:43
Funções
-
- [Funções] Domínio e a imagem de funções
 por concurseironf » Qui Ago 21, 2014 12:24
por concurseironf » Qui Ago 21, 2014 12:24
- 1 Respostas
- 4199 Exibições
- Última mensagem por Pessoa Estranha

Sex Ago 22, 2014 20:11
Funções
-
- [Funções] questões de funções
por Zandrojr » Qua Ago 31, 2011 11:39
- 0 Respostas
- 3141 Exibições
- Última mensagem por Zandrojr

Qua Ago 31, 2011 11:39
Funções
-
- Funções
por Revelants » Dom Out 05, 2008 15:07
- 1 Respostas
- 3392 Exibições
- Última mensagem por Molina

Dom Out 05, 2008 15:53
Cálculo: Limites, Derivadas e Integrais
-
- Funçoes
por Luna » Seg Set 28, 2009 20:02
- 1 Respostas
- 2998 Exibições
- Última mensagem por Marcampucio

Seg Set 28, 2009 21:35
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
zig - Sex Set 23, 2011 13:57
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
Vennom - Sex Set 23, 2011 21:41
zig escreveu:![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Rpz, o negócio é o seguinte:
Quando você tem uma potência negativa, tu deve inverter a base dela. Por exemplo:

Então pense o seguinte: a fração geratriz de 0,05 é

, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
Veja:
![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
A raiz quadrada de vinte, você acha fácil, né?
Espero ter ajudado.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:23
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:24
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.

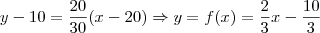
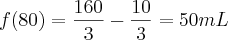
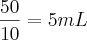


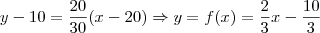
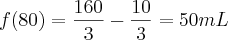
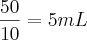





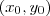 e tem coeficiente angular
e tem coeficiente angular  , veja:
, veja: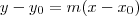






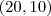 e
e 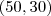 pertencem ao gráfico, ele escolheu o primeiro como
pertencem ao gráfico, ele escolheu o primeiro como 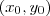 de referência, e o coeficiente angular é dado por
de referência, e o coeficiente angular é dado por 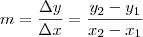 . Escolhendo os pontos dados, temos:
. Escolhendo os pontos dados, temos: 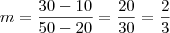 .
.


![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.