 por rhodry » Dom Nov 27, 2011 15:27
por rhodry » Dom Nov 27, 2011 15:27
Não estou conseguindo resolvê-la, se tiver alguém que poderá me ajudar agradeço...
2. Resolva a equaçao irracional:x+2
![\sqrt[]{4-x^2=4}} \sqrt[]{4-x^2=4}}](/latexrender/pictures/a8b5c3c82d26777258a4f29c5c9ecf69.png)
(Cuidado! Ao tratar equações irracionais é de maior importância ter em mente que, quando A>0, o simbolo
![\sqrt[]{A} \sqrt[]{A}](/latexrender/pictures/e45d117dfdaea89cb0d2449d76c19abc.png)
significa o número C positivo tal que
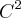
=A.)
-
rhodry
- Usuário Ativo

-
- Mensagens: 24
- Registrado em: Ter Out 25, 2011 17:59
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Matemática
- Andamento: cursando
 por Andreza » Dom Nov 27, 2011 15:36
por Andreza » Dom Nov 27, 2011 15:36
Vc tem a resposta do gabarito?
O 4 depois do sinal de igual nao está fora do radical?
-
Andreza
- Colaborador Voluntário

-
- Mensagens: 100
- Registrado em: Sáb Out 22, 2011 11:10
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Licenc. Plena Matemática
- Andamento: formado
 por rhodry » Dom Nov 27, 2011 15:38
por rhodry » Dom Nov 27, 2011 15:38
Não tenho Andreza,,,
-
rhodry
- Usuário Ativo

-
- Mensagens: 24
- Registrado em: Ter Out 25, 2011 17:59
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Matemática
- Andamento: cursando
 por LuizAquino » Seg Nov 28, 2011 20:36
por LuizAquino » Seg Nov 28, 2011 20:36
rhodry escreveu:2. Resolva a equaçao irracional:x+2
![\sqrt[]{4-x^2=4}} \sqrt[]{4-x^2=4}}](/latexrender/pictures/a8b5c3c82d26777258a4f29c5c9ecf69.png)
(Cuidado! Ao tratar equações irracionais é de maior importância ter em mente que, quando A>0, o simbolo
![\sqrt[]{A} \sqrt[]{A}](/latexrender/pictures/e45d117dfdaea89cb0d2449d76c19abc.png)
significa o número C positivo tal que

.)
Eu presumo que a equação seja na verdade:
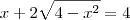
rhodry escreveu:Não estou conseguindo resolvê-la, se tiver alguém que poderá me ajudar agradeço...
Primeiro, como condição de existência para a solução no conjunto dos reais, precisamos que
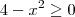
. Ou seja, devemos ter
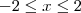
.
Supondo que x respeita essa condição, temos que:
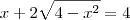

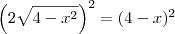

Agora termine o exercício.
Editado pela última vez por
LuizAquino em Ter Nov 29, 2011 09:36, em um total de 1 vez.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por vanessa_mat » Seg Nov 28, 2011 21:25
por vanessa_mat » Seg Nov 28, 2011 21:25
LuizAquino escreveu:rhodry escreveu:2. Resolva a equaçao irracional:x+2
![\sqrt[]{4-x^2=4}} \sqrt[]{4-x^2=4}}](/latexrender/pictures/a8b5c3c82d26777258a4f29c5c9ecf69.png)
(Cuidado! Ao tratar equações irracionais é de maior importância ter em mente que, quando A>0, o simbolo
![\sqrt[]{A} \sqrt[]{A}](/latexrender/pictures/e45d117dfdaea89cb0d2449d76c19abc.png)
significa o número C positivo tal que

.)
Eu presumo que a equação seja na verdade:
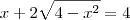
rhodry escreveu:Não estou conseguindo resolvê-la, se tiver alguém que poderá me ajudar agradeço...
Primeiro, como condição de existência para a solução no conjunto dos reais, precisamos que
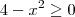
. Ou seja, devemos ter
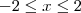
.
Supondo que x respeita essa condição, temos que:
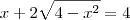

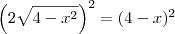

Agora termine o exercício.
porque não poderia começar elevando os dois membros ao quadrado sem mudar o x de lado!!
(x +2.\sqrt4-x^2)^2= 4^2[/tex]
-
vanessa_mat
- Usuário Ativo

-
- Mensagens: 18
- Registrado em: Seg Nov 21, 2011 16:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em matemática
- Andamento: formado
 por Rosana Vieira » Ter Nov 29, 2011 15:28
por Rosana Vieira » Ter Nov 29, 2011 15:28
LuizAquino escreveu:vanessa_mat escreveu:porque não poderia começar elevando os dois membros ao quadrado sem mudar o x de lado!!

Por um motivo muito simples: daria mais trabalho desse jeito.
Aplicando o que você disse e considerando que
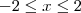
, temos que:

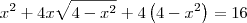
Agora teríamos que fazer:
A partir daqui estou certa ou errada
64x2+ 16x4 = 9x4
64x2+ 16x4 - 9x4 = 0
64x2 - 7 x4


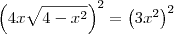

Agora continue a partir daqui.
-
Rosana Vieira
- Usuário Parceiro

-
- Mensagens: 74
- Registrado em: Qui Nov 17, 2011 00:11
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por Rosana Vieira » Ter Nov 29, 2011 15:35
por Rosana Vieira » Ter Nov 29, 2011 15:35
LuizAquino escreveu:rhodry escreveu:2. Resolva a equaçao irracional:x+2
![\sqrt[]{4-x^2=4}} \sqrt[]{4-x^2=4}}](/latexrender/pictures/a8b5c3c82d26777258a4f29c5c9ecf69.png)
(Cuidado! Ao tratar equações irracionais é de maior importância ter em mente que, quando A>0, o simbolo
![\sqrt[]{A} \sqrt[]{A}](/latexrender/pictures/e45d117dfdaea89cb0d2449d76c19abc.png)
significa o número C positivo tal que

.)
Eu presumo que a equação seja na verdade:
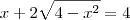
rhodry escreveu:Não estou conseguindo resolvê-la, se tiver alguém que poderá me ajudar agradeço...
Primeiro, como condição de existência para a solução no conjunto dos reais, precisamos que
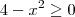
. Ou seja, devemos ter
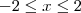
.
Supondo que x respeita essa condição, temos que:
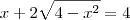

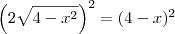

Agora termine o exercício.
A partir daqui está ou errada
15 x2 + 8x = 0
-
Rosana Vieira
- Usuário Parceiro

-
- Mensagens: 74
- Registrado em: Qui Nov 17, 2011 00:11
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por LuizAquino » Ter Nov 29, 2011 15:50
por LuizAquino » Ter Nov 29, 2011 15:50
Rosana Vieira escreveu:
A partir daqui estou certa ou errada
64x2+ 16x4 = 9x4
64x2+ 16x4 - 9x4 = 0
64x2 - 7 x4
Está errado. Note que:
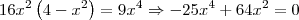
Rosana Vieira escreveu:
A partir daqui está ou errada
15 x2 + 8x = 0
Está errado. Note que:

-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Rosana Vieira » Ter Nov 29, 2011 16:04
por Rosana Vieira » Ter Nov 29, 2011 16:04
LuizAquino escreveu:Rosana Vieira escreveu:
A partir daqui estou certa ou errada
64x2+ 16x4 = 9x4
64x2+ 16x4 - 9x4 = 0
64x2 - 7 x4
Está errado. Note que:
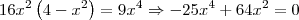
Rosana Vieira escreveu:
A partir daqui está ou errada
15 x2 + 8x = 0
Está errado. Note que:

conseguir fazer grato
-
Rosana Vieira
- Usuário Parceiro

-
- Mensagens: 74
- Registrado em: Qui Nov 17, 2011 00:11
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por vanessa_mat » Ter Nov 29, 2011 23:26
por vanessa_mat » Ter Nov 29, 2011 23:26
LuizAquino escreveu:vanessa_mat escreveu:porque não poderia começar elevando os dois membros ao quadrado sem mudar o x de lado!!

Por um motivo muito simples: daria mais trabalho desse jeito.
Aplicando o que você disse e considerando que
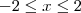
, temos que:

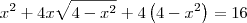
Agora teríamos que fazer:


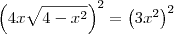

Agora continue a partir daqui.
Os meus valores estavam dando diferente das duas maneiras pois estava esquecendo de isolar o radical num dos membros da equação depois de resolver o produto notável. Obrigada
-
vanessa_mat
- Usuário Ativo

-
- Mensagens: 18
- Registrado em: Seg Nov 21, 2011 16:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em matemática
- Andamento: formado
 por vcbuldrini » Qui Dez 01, 2011 12:56
por vcbuldrini » Qui Dez 01, 2011 12:56
64 x2 - 25 x4 = 0
x2 = ?64/25
x= +- 8/5
ta certo isso .....
observação os tutores nao deixa trocarmos figurinha , mas o tutor copia do site so matematica as dicas dos exercicios resolvidos
-
vcbuldrini
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Seg Out 17, 2011 21:19
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: matematica
- Andamento: cursando
 por LuizAquino » Qui Dez 01, 2011 15:56
por LuizAquino » Qui Dez 01, 2011 15:56
vcbuldrini escreveu:64 x2 - 25 x4 = 0
x2 = ?64/25
x= +- 8/5
ta certo isso .....
Está incompleto.
Note que:
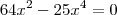
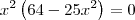
Temos então dois casos:
(i)

;
(ii)
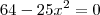
.
Resolvendo cada caso, no final temos que

e
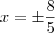
.
Substituindo esses valores na equação original (isto é,
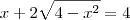
), temos que a solução final é apenas

.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por vcbuldrini » Qui Dez 01, 2011 19:53
por vcbuldrini » Qui Dez 01, 2011 19:53
agradeço desde ja
-
vcbuldrini
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Seg Out 17, 2011 21:19
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: matematica
- Andamento: cursando
Voltar para Sistemas de Equações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Equação Irracional
por luanxd » Ter Fev 09, 2010 23:44
- 2 Respostas
- 2081 Exibições
- Última mensagem por MarceloFantini

Qua Fev 10, 2010 12:38
Sistemas de Equações
-
- equação irracional
por Rosana Vieira » Ter Nov 29, 2011 13:51
- 1 Respostas
- 1608 Exibições
- Última mensagem por ivanfx

Ter Nov 29, 2011 15:04
Funções
-
- Equação irracional
por PeterHiggs » Sex Set 28, 2012 12:33
- 2 Respostas
- 1564 Exibições
- Última mensagem por PeterHiggs

Sex Set 28, 2012 22:14
Álgebra Elementar
-
- Equação irracional
por Flordelis25 » Sáb Abr 20, 2013 17:39
- 2 Respostas
- 1580 Exibições
- Última mensagem por Flordelis25

Sex Mai 24, 2013 17:17
Equações
-
- Equaçao Irracional
por Amanda91 » Qua Jul 10, 2013 03:05
- 3 Respostas
- 1831 Exibições
- Última mensagem por DanielFerreira

Sáb Nov 02, 2013 09:14
Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\sqrt[]{4-x^2=4}} \sqrt[]{4-x^2=4}}](/latexrender/pictures/a8b5c3c82d26777258a4f29c5c9ecf69.png)
![\sqrt[]{A} \sqrt[]{A}](/latexrender/pictures/e45d117dfdaea89cb0d2449d76c19abc.png) significa o número C positivo tal que
significa o número C positivo tal que 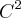 =A.)
=A.)
![\sqrt[]{4-x^2=4}} \sqrt[]{4-x^2=4}}](/latexrender/pictures/a8b5c3c82d26777258a4f29c5c9ecf69.png)
![\sqrt[]{A} \sqrt[]{A}](/latexrender/pictures/e45d117dfdaea89cb0d2449d76c19abc.png) significa o número C positivo tal que
significa o número C positivo tal que 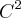 =A.)
=A.)


significa o número C positivo tal que
.)
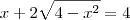
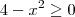 . Ou seja, devemos ter
. Ou seja, devemos ter 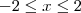 .
.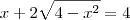

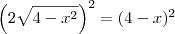


significa o número C positivo tal que
.)
. Ou seja, devemos ter
.

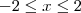 , temos que:
, temos que:
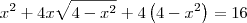


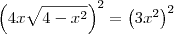


, temos que:

significa o número C positivo tal que
.)
. Ou seja, devemos ter
.

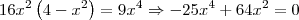



, temos que:


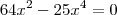
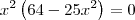
 ;
;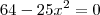 .
. e
e 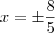 .
.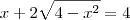 ), temos que a solução final é apenas
), temos que a solução final é apenas  .
.

 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
