 por beel » Dom Nov 27, 2011 21:00
por beel » Dom Nov 27, 2011 21:00
Pra achar o comprimento da curva(
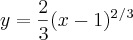
) que vai do ponto (1,0) a (2,2/3)
fiz
![\int_{a}^{b}\sqrt[]{1+f\prime(x)^2}dx \int_{a}^{b}\sqrt[]{1+f\prime(x)^2}dx](/latexrender/pictures/6ebbaa8f00f7d860da5c17a18cc1a969.png)
f'(x^)² =
![\frac{16}{81\sqrt[3]{(x-1)^2}} \frac{16}{81\sqrt[3]{(x-1)^2}}](/latexrender/pictures/84523ee3820ac7b335df3cfd3d240650.png)
,
ai preciso resolver essa integral, mas como acho a primitiva disso pra resolver?
e quais seriam os limites de integração?
-
beel
- Colaborador Voluntário

-
- Mensagens: 172
- Registrado em: Sex Ago 26, 2011 13:14
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por TheoFerraz » Seg Nov 28, 2011 14:38
por TheoFerraz » Seg Nov 28, 2011 14:38
os limites de integração seriam os valores do eixo x de cada ponto.
achar a primitiva pode ser meio complicado, o que voce pode fazer é ir no site www.wolframalpha.com
e digitar no box:
integrate {função que quero integrar}
Exemplo:
integrate 1/(x-2)
depois clique no botão "Show steps" ele te mostrará todos os passos que usou para calcular a integral.
-
TheoFerraz
- Colaborador Voluntário

-
- Mensagens: 107
- Registrado em: Qua Abr 13, 2011 19:23
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Bacharelado em Física
- Andamento: cursando
 por beel » Ter Nov 29, 2011 16:56
por beel » Ter Nov 29, 2011 16:56
O problema é se cair isso numa prova, ai estou lascada (:
nao tem como simplificar ou alguma coisa do tipo?
-
beel
- Colaborador Voluntário

-
- Mensagens: 172
- Registrado em: Sex Ago 26, 2011 13:14
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por TheoFerraz » Ter Nov 29, 2011 17:36
por TheoFerraz » Ter Nov 29, 2011 17:36
O site que eu passei não daria a resposta de mão beijada simplesmente. ele daria justamente o que voce quer, as simplificações necessárias.... Todas as trocas de variável que se deve fazer uma por uma e todo o processo descrito!
ao clicar no botão "show steps" ele mostrará os passos utilizados, todas as simplificações.
Eu não faço aqui pois essa integral vai demorar uma vida pra escrever aqui no forum! faz mais sentido voce ir lá e ver os passos. mas se fizer questão eu faço...
-
TheoFerraz
- Colaborador Voluntário

-
- Mensagens: 107
- Registrado em: Qua Abr 13, 2011 19:23
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Bacharelado em Física
- Andamento: cursando
 por beel » Dom Dez 04, 2011 21:30
por beel » Dom Dez 04, 2011 21:30
aaa sim...nao,nao é necessario, obrigada.
-
beel
- Colaborador Voluntário

-
- Mensagens: 172
- Registrado em: Sex Ago 26, 2011 13:14
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Integral] Comprimento de Arco
por klueger » Qui Mar 21, 2013 10:19
- 5 Respostas
- 3402 Exibições
- Última mensagem por Russman

Qui Mar 21, 2013 12:54
Cálculo: Limites, Derivadas e Integrais
-
- [Integral] Arco tangente
por KleinIll » Seg Mar 25, 2013 13:27
- 2 Respostas
- 2872 Exibições
- Última mensagem por KleinIll

Seg Mar 25, 2013 19:07
Cálculo: Limites, Derivadas e Integrais
-
- Calculo do comprimento do arco.
por brunojorge29 » Seg Abr 23, 2012 11:21
- 3 Respostas
- 2959 Exibições
- Última mensagem por Russman

Seg Abr 23, 2012 22:32
Cálculo: Limites, Derivadas e Integrais
-
- Integral para calcular arco
por neoreload » Sex Mar 20, 2015 07:04
- 2 Respostas
- 3203 Exibições
- Última mensagem por Russman

Seg Mar 23, 2015 01:55
Cálculo: Limites, Derivadas e Integrais
-
- [integral] questao sobre arco da curva
por sabrinasilveira » Seg Jun 29, 2015 00:11
- 0 Respostas
- 1558 Exibições
- Última mensagem por sabrinasilveira

Seg Jun 29, 2015 00:11
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 5 visitantes
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 10:38
Olá ! Tenho essa dúvida e não consigo montar o problema para resolução:
Qual é o racional não nulo cujo o quadrado é igual à sua terça parte ?
Grata.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 12:27

Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 12:55
também pensei que fosse assim, mas a resposta é

.
Obrigada Fantini.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 13:01

Como

:

O que você fez?
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 16:17
eu só consegui fazer a igualdade, não consegui desenvolver o restante, não pensei em fatoração, mas agora entendi o que vc fez.
Obrigada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
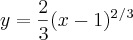 ) que vai do ponto (1,0) a (2,2/3)
) que vai do ponto (1,0) a (2,2/3) ![\int_{a}^{b}\sqrt[]{1+f\prime(x)^2}dx \int_{a}^{b}\sqrt[]{1+f\prime(x)^2}dx](/latexrender/pictures/6ebbaa8f00f7d860da5c17a18cc1a969.png)
![\frac{16}{81\sqrt[3]{(x-1)^2}} \frac{16}{81\sqrt[3]{(x-1)^2}}](/latexrender/pictures/84523ee3820ac7b335df3cfd3d240650.png) ,
,
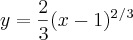 ) que vai do ponto (1,0) a (2,2/3)
) que vai do ponto (1,0) a (2,2/3) ![\int_{a}^{b}\sqrt[]{1+f\prime(x)^2}dx \int_{a}^{b}\sqrt[]{1+f\prime(x)^2}dx](/latexrender/pictures/6ebbaa8f00f7d860da5c17a18cc1a969.png)
![\frac{16}{81\sqrt[3]{(x-1)^2}} \frac{16}{81\sqrt[3]{(x-1)^2}}](/latexrender/pictures/84523ee3820ac7b335df3cfd3d240650.png) ,
,





 .
.
 :
: