 por beel » Dom Nov 20, 2011 22:38
por beel » Dom Nov 20, 2011 22:38

, nessa integral,fiz por substituiçao e tomei o "u" como 1/x...
so fiquei em duvida no final...eu substitui os extremos da integrada e meu resultado deu
e^1/2 - e^1/3...se nao substituir os extremos a resposta seria e^2-e^3 e tem essa opçao como resposta
-
beel
- Colaborador Voluntário

-
- Mensagens: 172
- Registrado em: Sex Ago 26, 2011 13:14
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por LuizAquino » Seg Nov 21, 2011 09:58
por LuizAquino » Seg Nov 21, 2011 09:58
beel escreveu: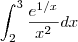
, nessa integral,fiz por substituiçao e tomei o "u" como 1/x...
so fiquei em duvida no final...eu substitui os extremos da integrada e meu resultado deu
e^1/2 - e^1/3...se nao substituir os extremos a resposta seria e^2-e^3 e tem essa opçao como resposta
Para conferir sua resolução, siga os procedimentos abaixo.
Parte 1) Estudar o desenvolvimento de
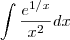
.
- Acesse a página: http://www.wolframalpha.com/
- No campo de entrada, digite:
- Código: Selecionar todos
integrate e^(1/x)/(x^2) dx
- Clique no botão de igual ao lado do campo de entrada.
- Após a integral ser calculada, clique no botão "Show steps" ao lado do resultado.
- Pronto! Agora basta estudar a resolução e comparar com a sua.
Parte 2) Calcular o valor de
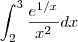
.
- Acesse a página: http://www.wolframalpha.com/
- No campo de entrada, digite:
- Código: Selecionar todos
integrate e^(1/x)/(x^2) dx x=2..3
- Clique no botão de igual ao lado do campo de entrada.
- Após o processamento irá aparecer o valor dessa integral definida.
- Pronto! Agora basta comparar o valor com o resultado obtido por você.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por beel » Ter Nov 22, 2011 15:50
por beel » Ter Nov 22, 2011 15:50
-
beel
- Colaborador Voluntário

-
- Mensagens: 172
- Registrado em: Sex Ago 26, 2011 13:14
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por LuizAquino » Ter Nov 22, 2011 16:55
por LuizAquino » Ter Nov 22, 2011 16:55
beel escreveu:uma pergunta,
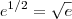
, e
![e^{1/3} = \sqrt[3]{e} e^{1/3} = \sqrt[3]{e}](/latexrender/pictures/0ffc3fd2c8887238d60d3d1e00d6b3a3.png)
?
Sim.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [calculo] integral definida
por beel » Sex Nov 18, 2011 12:29
- 1 Respostas
- 1837 Exibições
- Última mensagem por LuizAquino

Sex Nov 18, 2011 22:05
Cálculo: Limites, Derivadas e Integrais
-
- [calculo] integral definida
por beel » Sex Nov 18, 2011 12:48
- 1 Respostas
- 1979 Exibições
- Última mensagem por LuizAquino

Sex Nov 18, 2011 22:07
Cálculo: Limites, Derivadas e Integrais
-
- [calculo] integral definida
por beel » Sex Nov 18, 2011 12:53
- 1 Respostas
- 2015 Exibições
- Última mensagem por LuizAquino

Sex Nov 18, 2011 22:00
Cálculo: Limites, Derivadas e Integrais
-
- [calculo] integral definida
por beel » Sex Nov 18, 2011 13:29
- 1 Respostas
- 1718 Exibições
- Última mensagem por MarceloFantini

Sex Nov 18, 2011 16:18
Cálculo: Limites, Derivadas e Integrais
-
- Calculo de Integral definida..
por Nei Stolberg » Qui Mar 21, 2019 19:11
- 0 Respostas
- 4725 Exibições
- Última mensagem por Nei Stolberg

Qui Mar 21, 2019 19:11
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 4 visitantes
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 , nessa integral,fiz por substituiçao e tomei o "u" como 1/x...
, nessa integral,fiz por substituiçao e tomei o "u" como 1/x...

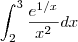 , nessa integral,fiz por substituiçao e tomei o "u" como 1/x...
, nessa integral,fiz por substituiçao e tomei o "u" como 1/x...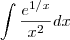 .
.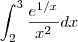 .
.
 =
=![\sqrt[]{e} \sqrt[]{e}](/latexrender/pictures/6b648f67f137df801bc883cab7d4a113.png) , e
, e  =
=![\sqrt[3]{e} \sqrt[3]{e}](/latexrender/pictures/fbf1ec86e8fd79251b9fa5725d7b74d7.png) ?
?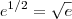 , e
, e ![e^{1/3} = \sqrt[3]{e} e^{1/3} = \sqrt[3]{e}](/latexrender/pictures/0ffc3fd2c8887238d60d3d1e00d6b3a3.png) ?
? .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
