Sabendo que sen x = 2 cos x e 0<x>pi /2, calcule
a) SEN 2X
eu tentei fazer através da fórmula sen 2x = 2sen x *cos x
sen 2x = 2 (2 cos x ) * cos x
sen 2x = 4 cos x * cos x
sen 2x = 4 cos ²x
e fui seguindo até chegar em baskara que naum dá o resultado certo
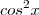por algo em função de seno.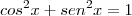
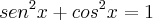encontramos:
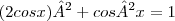Resolvendo: ![cosx=\frac{\sqrt[2]{5}}{5}](/latexrender/pictures/a6006ed89753cfec1016781a40188a7d.png "cosx=\frac{\sqrt[2]{5}}{5}")
![senx=\frac{\sqrt[2]{5}}{5}](/latexrender/pictures/fca457b1c784e825039a9dfa3c8eb1f3.png "senx=\frac{\sqrt[2]{5}}{5}")
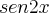, veja que é o mesmo que: 
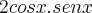. Como o cosseno e o seno de x é igual a ![\frac{\sqrt[2]{5}}{5}](/latexrender/pictures/598082af053f8185a4f3e69d70bce5cf.png "\frac{\sqrt[2]{5}}{5}")
é só substituí-los.
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png "\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}")
![\sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png "\sqrt[]{2}")
e elevar ao quadrado os dois lados)