 por Buda » Seg Out 24, 2011 21:28
por Buda » Seg Out 24, 2011 21:28
Ola. Preciso de ajuda quanto a esta sequencia.Se ela converge ou diverge.
an = cos(n/2) , e tambem aproveitando an = arctan(2n)
-
Buda
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Seg Out 24, 2011 21:18
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Mecanica
- Andamento: cursando
 por LuizAquino » Qua Out 26, 2011 00:35
por LuizAquino » Qua Out 26, 2011 00:35
Buda escreveu:an = cos(n/2)
Sabemos que toda sequência periódica convergente é constante.
Como essa sequência é periódica, se ela convergisse deveria ser constante. Mas, ela claramente não é constante. Portanto, ela é divergente.
Buda escreveu:an = arctan(2n)
Essa sequência é monótona (crescente) e limitada. Portanto ela é convergente.
Além disso, dos conhecimentos sobre a função arco-tangente, podemos dizer que o valor para o qual essa sequência converge é

.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Buda » Sáb Out 29, 2011 19:50
por Buda » Sáb Out 29, 2011 19:50
humm.. tendi brigado.
Agora , para as outras sequencias.Tambem qnt se diverge ou converge.
1) ln(n)/(ln (2n))
2) ln(n +1) - ln (n)
3) sen(2n)/ ( 1 + n^0.5)
Desculpe tantas perguntas.Mais eu nao entendi muito bem como faço.Se uso limite tendendo a infito.Ou se uso propriedade de logaritmo.
Desde ja obrigado.
-
Buda
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Seg Out 24, 2011 21:18
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Mecanica
- Andamento: cursando
 por LuizAquino » Sáb Out 29, 2011 20:31
por LuizAquino » Sáb Out 29, 2011 20:31
Buda escreveu:1) ln(n)/(ln (2n))
Converge.




Buda escreveu:2) ln(n +1) - ln (n)
Converge.
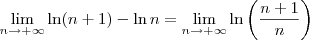


Buda escreveu:3) sen(2n)/ ( 1 + n^0.5)
Converge.
Sabemos que:

.
Multiplicando toda essa inequação pelo número positivo

, temos que:
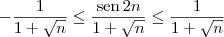
Sabemos que:
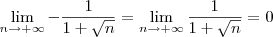
Pelo
Teorema do Confronto (ou Teorema do Sanduíche), segue que:
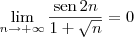
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Buda » Sáb Out 29, 2011 21:55
por Buda » Sáb Out 29, 2011 21:55
Nossa caramba. muito obrigado .Sem puxa saco, mais voce manja muito.
Tava vendo aki alguns exerciccios e teoria tava em duvida entre sequencia e serie, mais agora entendi a diferença.Agora teve um exercicio q fiquei em duvida.Vo tenta se meio resumido.Me corrija se estiver errado por favor.
tem a serie.
? n=1 ate infito positivo de 1/(2n) - que é uma serie harmonica que diverge.
E eu estava confundindo a harmonica com a geometrica.
Poderia me responder qual é mais ou menos o corpo de uma serie harmonica.Para saber que ja ira divegir de uma vez.Pois apliquei a formula de geometrica naquela serie harmonica e da 2. ? ar^(n-1) = a/(1-r) IrI <1 .Logicamente deu errado pois nao é geometrica e sim harmonica. E aplicando a formula do Teste da divergencia dava 2 que é diferente de 0 portanto diverge.
Enfim. Quando eu sei q a sequencia é harmonica ou geometrica????
-
Buda
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Seg Out 24, 2011 21:18
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Mecanica
- Andamento: cursando
 por LuizAquino » Sáb Out 29, 2011 22:38
por LuizAquino » Sáb Out 29, 2011 22:38
Buda escreveu:E eu estava confundindo a harmonica com a geometrica. (...)
Poderia me responder qual é mais ou menos o corpo de uma serie harmonica. (...)
Quando eu sei q a sequencia é harmonica ou geometrica?
Eu recomendo que você leia as páginas abaixo.
Série harmônicahttp://pt.wikipedia.org/wiki/S%C3%A9rie ... %A1tica%29Série geométricahttp://pt.wikipedia.org/wiki/S%C3%A9rie_geom%C3%A9trica
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Buda » Sáb Out 29, 2011 23:52
por Buda » Sáb Out 29, 2011 23:52
nao consegui ainda entende o meu problema.
a serie ? n=1 ate infinito positivo da funçao 1/(2n) .Que é uma serie harmonica(sempre diverge)
Mais fazendo o lim da funçao(teste da divergencia) da 1 sobre infinito = 0 ou seja converge????
Nao entendi???
-
Buda
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Seg Out 24, 2011 21:18
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Mecanica
- Andamento: cursando
 por Buda » Dom Out 30, 2011 00:27
por Buda » Dom Out 30, 2011 00:27
Segue as seguintes series. Determine se converge ou diverge. Qual é o massete ?
? de n=1 ate infinito positivo da funçao 3^(n) + 2^(n)/(6)^n
? de n=1 ate infinito positivo da funçao ln((n^2 + 1)/(2n^2 +1))
? de n=1 ate infinito positivo da funçao e^n/n^2
obrigado
-
Buda
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Seg Out 24, 2011 21:18
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Mecanica
- Andamento: cursando
 por MarceloFantini » Dom Out 30, 2011 03:34
por MarceloFantini » Dom Out 30, 2011 03:34
Séries harmônicas são da forma

, com

. Para
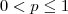
, ela diverge. Para

, ela converge.
A série geométrica é a série da forma

com

.
Para testar se um série converge, faça o limite da sequência da série com

. Se o limite for zero, ela
pode convergir, mas se o limite for diferente de zero então
com certeza ela diverge.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por LuizAquino » Dom Out 30, 2011 13:00
por LuizAquino » Dom Out 30, 2011 13:00
Eu recomendo que você leia a página:
Série (matemática)http://pt.wikipedia.org/wiki/S%C3%A9rie ... %A1tica%29Nesse texto há uma seção tratando sobre os testes de convergência ou divergência de séries.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Buda » Dom Out 30, 2011 19:05
por Buda » Dom Out 30, 2011 19:05
Poderia me ajudar com essa estimativa de serie.obrigado
Encontre a soma parcial s10 da serie ? n=1 ate infinito positivo 1/((n)^4) . Estime o erro cometido ao usar s10 como uma aproximaçao para a soma da serie.
Encontre uma valor de n tal que sn represente a soma com precisao de 0,00001.
-
Buda
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Seg Out 24, 2011 21:18
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Mecanica
- Andamento: cursando
 por LuizAquino » Qua Nov 02, 2011 11:15
por LuizAquino » Qua Nov 02, 2011 11:15
Buda escreveu:Encontre a soma parcial s10 da serie ? n=1 ate infinito positivo 1/((n)^4) . Estime o erro cometido ao usar s10 como uma aproximaçao para a soma da serie.
Encontre uma valor de n tal que sn represente a soma com precisao de 0,00001.
Esse exercício é uma aplicação direta da
"Estimativa do erro para o Teste da Integral". Você já estudou esse conteúdo?
Se você já estudou, então qual foi a sua dificuldade nesse exercício?
Por outro lado, se você ainda não estudou, então eu recomendo que estude esse conteúdo antes de tentar esse exercício.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Sequências
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Série converge ou diverge
por Crist » Seg Fev 25, 2013 21:51
- 2 Respostas
- 2365 Exibições
- Última mensagem por Crist

Sáb Mar 02, 2013 10:16
Sequências
-
- Integral: converge ou diverge
por Victor Gabriel » Qui Abr 18, 2013 13:24
- 1 Respostas
- 1009 Exibições
- Última mensagem por Victor Gabriel

Dom Abr 21, 2013 12:03
Cálculo: Limites, Derivadas e Integrais
-
- Integral: converge
por Victor Gabriel » Seg Abr 29, 2013 14:57
- 0 Respostas
- 870 Exibições
- Última mensagem por Victor Gabriel

Seg Abr 29, 2013 14:57
Cálculo: Limites, Derivadas e Integrais
-
- [sequencia] Calcular limite de sequencia por definição
 por amigao » Ter Abr 15, 2014 15:15
por amigao » Ter Abr 15, 2014 15:15
- 4 Respostas
- 3997 Exibições
- Última mensagem por e8group

Dom Mai 11, 2014 17:09
Sequências
-
- Sequencia
por Amparo » Dom Mar 09, 2008 16:26
- 3 Respostas
- 3597 Exibições
- Última mensagem por nietzsche

Sex Set 02, 2011 00:42
Sequências
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



 .
.





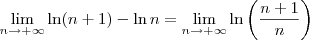


 .
. , temos que:
, temos que: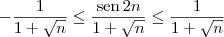
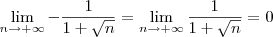
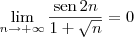





 , com
, com  . Para
. Para 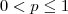 , ela diverge. Para
, ela diverge. Para  , ela converge.
, ela converge. com
com  .
. . Se o limite for zero, ela pode convergir, mas se o limite for diferente de zero então com certeza ela diverge.
. Se o limite for zero, ela pode convergir, mas se o limite for diferente de zero então com certeza ela diverge.



