Ola. Preciso de ajuda quanto a esta sequencia.Se ela converge ou diverge.
an = cos(n/2) , e tambem aproveitando an = arctan(2n)



Buda escreveu:an = cos(n/2)
Buda escreveu:an = arctan(2n)
 .
.

Buda escreveu:1) ln(n)/(ln (2n))




Buda escreveu:2) ln(n +1) - ln (n)
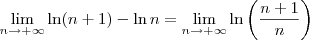


Buda escreveu:3) sen(2n)/ ( 1 + n^0.5)
 .
. , temos que:
, temos que: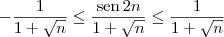
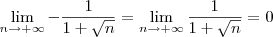
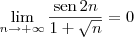


Buda escreveu:E eu estava confundindo a harmonica com a geometrica. (...)
Poderia me responder qual é mais ou menos o corpo de uma serie harmonica. (...)
Quando eu sei q a sequencia é harmonica ou geometrica?



 , com
, com  . Para
. Para 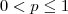 , ela diverge. Para
, ela diverge. Para  , ela converge.
, ela converge. com
com  .
. . Se o limite for zero, ela pode convergir, mas se o limite for diferente de zero então com certeza ela diverge.
. Se o limite for zero, ela pode convergir, mas se o limite for diferente de zero então com certeza ela diverge.



Buda escreveu:Encontre a soma parcial s10 da serie ? n=1 ate infinito positivo 1/((n)^4) . Estime o erro cometido ao usar s10 como uma aproximaçao para a soma da serie.
Encontre uma valor de n tal que sn represente a soma com precisao de 0,00001.

Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)