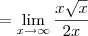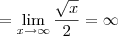por beel » Seg Out 24, 2011 17:18
por beel » Seg Out 24, 2011 17:18
limite de
![\lim_{x\rightarrow\infty}\frac{\sqrt[]{x}}{lnx}
seria
\lim_{x\rightarrow\infty}\frac{\sqrt[]{x}\prime}{(lnx)\prime} =
\lim_{x\rightarrow\infty}\frac{2\sqrt[]{x}}{x} (L'Hospital novamente) =
\lim_{x\rightarrow\infty}\frac{1}{\sqrt[]{x}} = 0 \lim_{x\rightarrow\infty}\frac{\sqrt[]{x}}{lnx}
seria
\lim_{x\rightarrow\infty}\frac{\sqrt[]{x}\prime}{(lnx)\prime} =
\lim_{x\rightarrow\infty}\frac{2\sqrt[]{x}}{x} (L'Hospital novamente) =
\lim_{x\rightarrow\infty}\frac{1}{\sqrt[]{x}} = 0](/latexrender/pictures/437a9b7e609ee02e30384df71ca65099.png)
?
-
beel
- Colaborador Voluntário

-
- Mensagens: 172
- Registrado em: Sex Ago 26, 2011 13:14
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por LuizAquino » Seg Out 24, 2011 17:59
por LuizAquino » Seg Out 24, 2011 17:59
BEL NS escreveu:limite de
![\lim_{x\rightarrow\infty}\frac{\sqrt[]{x}}{lnx} \lim_{x\rightarrow\infty}\frac{\sqrt[]{x}}{lnx}](/latexrender/pictures/db84407b52df7fc7329d8c79993df1be.png)
seria
![\lim_{x\rightarrow\infty}\frac{\sqrt[]{x}\prime}{(lnx)\prime} = \lim_{x\rightarrow\infty}\frac{\sqrt[]{x}\prime}{(lnx)\prime} =](/latexrender/pictures/8fe2dd2b841070936fb8bda85fafeaf0.png)
![\lim_{x\rightarrow\infty}\frac{2\sqrt[]{x}}{x} = \lim_{x\rightarrow\infty}\frac{2\sqrt[]{x}}{x} =](/latexrender/pictures/c1e94ff9199458bb957fdbfceb5baec2.png)
(L'Hospital novamente)
![\lim_{x\rightarrow\infty}\frac{1}{\sqrt[]{x}} = 0 \lim_{x\rightarrow\infty}\frac{1}{\sqrt[]{x}} = 0](/latexrender/pictures/25eed37d2a944eacba24d2ab0352aebe.png)
[/tex]
?
Note que:

Agora tente terminar o exercício.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por beel » Ter Out 25, 2011 17:12
por beel » Ter Out 25, 2011 17:12
seria...
![\lim_{x\rightarrow\infty}\frac{(x)\prime}{(2\sqrt[]{x})\prime} =
\lim_{x\rightarrow\infty}\frac{1}{\frac{1}{\sqrt[]{x}}} = \lim_{x\rightarrow\infty}\sqrt[]{x} \lim_{x\rightarrow\infty}\frac{(x)\prime}{(2\sqrt[]{x})\prime} =
\lim_{x\rightarrow\infty}\frac{1}{\frac{1}{\sqrt[]{x}}} = \lim_{x\rightarrow\infty}\sqrt[]{x}](/latexrender/pictures/1fcaf18e3cd44718aa39a3506d535cfd.png)
a resposta seria

?
-
beel
- Colaborador Voluntário

-
- Mensagens: 172
- Registrado em: Sex Ago 26, 2011 13:14
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [CALCULO] limite - L'Hospital?
por beel » Dom Out 30, 2011 17:13
- 3 Respostas
- 1907 Exibições
- Última mensagem por LuizAquino

Dom Out 30, 2011 18:28
Cálculo: Limites, Derivadas e Integrais
-
- Limite( Cálculo de limites sem a utilização L'hôspital )
 por brunotorres123-abc » Dom Abr 05, 2015 14:55
por brunotorres123-abc » Dom Abr 05, 2015 14:55
- 0 Respostas
- 1153 Exibições
- Última mensagem por brunotorres123-abc

Dom Abr 05, 2015 14:55
Cálculo: Limites, Derivadas e Integrais
-
- LIMITE COM L HOSPITAL
por geovane » Seg Out 03, 2016 18:17
- 1 Respostas
- 5211 Exibições
- Última mensagem por DanielFerreira

Sáb Nov 26, 2016 19:03
Cálculo: Limites, Derivadas e Integrais
-
- Resolver limite de exponencial por L'Hospital.
 por Sobreira » Sáb Nov 30, 2013 15:00
por Sobreira » Sáb Nov 30, 2013 15:00
- 9 Respostas
- 6558 Exibições
- Última mensagem por e8group

Sáb Nov 30, 2013 17:37
Cálculo: Limites, Derivadas e Integrais
-
- [Limite trigonométrico] Como calculo este limite?
por Ronaldobb » Qua Nov 07, 2012 23:14
- 3 Respostas
- 5121 Exibições
- Última mensagem por Ronaldobb

Qui Nov 08, 2012 07:37
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\lim_{x\rightarrow\infty}\frac{\sqrt[]{x}}{lnx}
seria
\lim_{x\rightarrow\infty}\frac{\sqrt[]{x}\prime}{(lnx)\prime} =
\lim_{x\rightarrow\infty}\frac{2\sqrt[]{x}}{x} (L'Hospital novamente) =
\lim_{x\rightarrow\infty}\frac{1}{\sqrt[]{x}} = 0 \lim_{x\rightarrow\infty}\frac{\sqrt[]{x}}{lnx}
seria
\lim_{x\rightarrow\infty}\frac{\sqrt[]{x}\prime}{(lnx)\prime} =
\lim_{x\rightarrow\infty}\frac{2\sqrt[]{x}}{x} (L'Hospital novamente) =
\lim_{x\rightarrow\infty}\frac{1}{\sqrt[]{x}} = 0](/latexrender/pictures/437a9b7e609ee02e30384df71ca65099.png)

![\lim_{x\rightarrow\infty}\frac{\sqrt[]{x}}{lnx}
seria
\lim_{x\rightarrow\infty}\frac{\sqrt[]{x}\prime}{(lnx)\prime} =
\lim_{x\rightarrow\infty}\frac{2\sqrt[]{x}}{x} (L'Hospital novamente) =
\lim_{x\rightarrow\infty}\frac{1}{\sqrt[]{x}} = 0 \lim_{x\rightarrow\infty}\frac{\sqrt[]{x}}{lnx}
seria
\lim_{x\rightarrow\infty}\frac{\sqrt[]{x}\prime}{(lnx)\prime} =
\lim_{x\rightarrow\infty}\frac{2\sqrt[]{x}}{x} (L'Hospital novamente) =
\lim_{x\rightarrow\infty}\frac{1}{\sqrt[]{x}} = 0](/latexrender/pictures/437a9b7e609ee02e30384df71ca65099.png)

[/tex]


![\lim_{x\rightarrow\infty}\frac{(x)\prime}{(2\sqrt[]{x})\prime} =
\lim_{x\rightarrow\infty}\frac{1}{\frac{1}{\sqrt[]{x}}} = \lim_{x\rightarrow\infty}\sqrt[]{x} \lim_{x\rightarrow\infty}\frac{(x)\prime}{(2\sqrt[]{x})\prime} =
\lim_{x\rightarrow\infty}\frac{1}{\frac{1}{\sqrt[]{x}}} = \lim_{x\rightarrow\infty}\sqrt[]{x}](/latexrender/pictures/1fcaf18e3cd44718aa39a3506d535cfd.png)
 ?
?
?