 por mausim » Ter Out 25, 2011 11:34
por mausim » Ter Out 25, 2011 11:34
Amigos, tentei resolver sozinho, mas não entendi o resultado que me deram. Não cheguei até ele.
Eu tenho a função
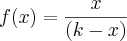
Quando eu derivo, encontro
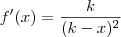
mas um programa que deriva funções na web me dá
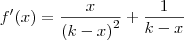
Eu fiz o procedimento através do desenvolvimento clássico, aquele que começa por

etc. etc...
e achei o meu resultado.
Onde será que cometi o erro?
Grato
-
mausim
- Usuário Ativo

-
- Mensagens: 15
- Registrado em: Ter Out 25, 2011 10:27
- Formação Escolar: SUPLETIVO
- Andamento: formado
 por LuizAquino » Ter Out 25, 2011 12:11
por LuizAquino » Ter Out 25, 2011 12:11
mausim escreveu:Quando eu derivo, encontro
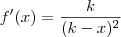
mas um programa que deriva funções na web me dá
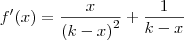
Some as duas frações que aparecem nessa segunda resposta e veja o que acontece. Lembre-se que o m. m. c. nesse caso será
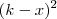
.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por mausim » Ter Out 25, 2011 12:23
por mausim » Ter Out 25, 2011 12:23
LuizAquino escreveu:mausim escreveu:Quando eu derivo, encontro
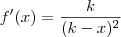
mas um programa que deriva funções na web me dá
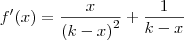
Some as duas frações que aparecem nessa segunda resposta e veja o que acontece. Lembre-se que o m. m. c. nesse caso será
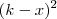
.
Luiz Aquino, desculpa a vergonha que passei, coisa primária. Obrigado pela ajuda. Fazendo sua sugestão, encontrei
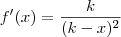
que era exatamente o que eu tinha calculado.
Muito obrigado.
Agora, uma pergunta: por que será que o programa desmembrou a fórmula? Será que, tecnicamente, é a forma correta de responder?
-
mausim
- Usuário Ativo

-
- Mensagens: 15
- Registrado em: Ter Out 25, 2011 10:27
- Formação Escolar: SUPLETIVO
- Andamento: formado
 por LuizAquino » Ter Out 25, 2011 12:51
por LuizAquino » Ter Out 25, 2011 12:51
mausim escreveu:Agora, uma pergunta: por que será que o programa desmembrou a fórmula?
Porque o programador quis assim!

mausim escreveu:Será que, tecnicamente, é a forma correta de responder?
Não. É simplesmente uma outra forma de escrever.
De qualquer modo, seria bem mais provável (em um livro, por exemplo) encontrar a derivada na forma que você escreveu do que na forma exibida pelo programa.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Cálculo: Limites, Derivadas e Integrais] Como resolver?
por IlgssonBraga » Seg Jan 20, 2014 16:40
- 1 Respostas
- 2030 Exibições
- Última mensagem por IlgssonBraga

Seg Jan 20, 2014 17:02
Cálculo: Limites, Derivadas e Integrais
-
- [Cálculo: Limites, Derivadas e Integrais] Cálculo de limites
por jeferson lopes » Ter Mar 26, 2013 08:49
- 2 Respostas
- 5569 Exibições
- Última mensagem por jeferson lopes

Ter Mar 26, 2013 11:52
Cálculo: Limites, Derivadas e Integrais
-
- [Derivadas/Integrais] Ajuda com 5 questões de cálculo
por matheuskns » Sex Nov 28, 2014 20:27
- 1 Respostas
- 1877 Exibições
- Última mensagem por Cleyson007

Sáb Nov 29, 2014 20:40
Cálculo: Limites, Derivadas e Integrais
-
- [DERIVADAS] Exercicios de derivação
por bencz » Seg Mar 14, 2016 12:56
- 1 Respostas
- 3025 Exibições
- Última mensagem por adauto martins

Seg Mar 14, 2016 19:07
Cálculo: Limites, Derivadas e Integrais
-
- Cálculo 1- Derivação
por johnatta » Sex Jun 12, 2015 10:32
- 1 Respostas
- 1561 Exibições
- Última mensagem por nakagumahissao

Sex Jun 12, 2015 14:52
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
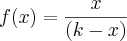
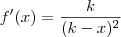
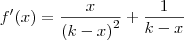
 etc. etc...
etc. etc...

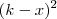 .
.
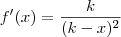



 , avisa que eu resolvo.
, avisa que eu resolvo.

