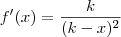[Cálculo: Limites, Derivadas e Integrais] - Derivação de quo

por **mausim** » Ter Out 25, 2011 11:34

Amigos, tentei resolver sozinho, mas não entendi o resultado que me deram. Não cheguei até ele.

Eu tenho a função

$f(x) = {x \over (k-x)}$

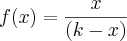
Quando eu derivo, encontro

$f'(x) = {k \over {(k-x)^2}}$

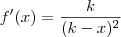
mas um programa que deriva funções na web me dá

$f'(x) = { x \over {(k-x)}^2} + {1 \over {k-x}}$

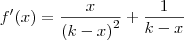
Eu fiz o procedimento através do desenvolvimento clássico, aquele que começa por

$y+\Delta y = {x + \Delta x}$ etc. etc...

e achei o meu resultado.

Onde será que cometi o erro?

Grato

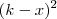por **LuizAquino** » Ter Out 25, 2011 12:11

mausim escreveu:Quando eu derivo, encontro

$f'(x) = {k \over {(k-x)^2}}$

mas um programa que deriva funções na web me dá

$f'(x) = { x \over {(k-x)}^2} + {1 \over {k-x}}$

Some as duas frações que aparecem nessa segunda resposta e veja o que acontece. Lembre-se que o m. m. c. nesse caso será (k-x)^2

.

por **mausim** » Ter Out 25, 2011 12:23

LuizAquino escreveu:
mausim escreveu:Quando eu derivo, encontro

$f'(x) = {k \over {(k-x)^2}}$

mas um programa que deriva funções na web me dá

$f'(x) = { x \over {(k-x)}^2} + {1 \over {k-x}}$

Some as duas frações que aparecem nessa segunda resposta e veja o que acontece. Lembre-se que o m. m. c. nesse caso será .

Luiz Aquino, desculpa a vergonha que passei, coisa primária. Obrigado pela ajuda. Fazendo sua sugestão, encontrei

$f'(x) = {k \over {(k-x)^2}$

que era exatamente o que eu tinha calculado.

Muito obrigado.

Agora, uma pergunta: por que será que o programa desmembrou a fórmula? Será que, tecnicamente, é a forma correta de responder?

por **LuizAquino** » Ter Out 25, 2011 12:51

mausim escreveu:Agora, uma pergunta: por que será que o programa desmembrou a fórmula?

Porque o programador quis assim!

mausim escreveu:Será que, tecnicamente, é a forma correta de responder?

Não. É simplesmente uma outra forma de escrever.

De qualquer modo, seria bem mais provável (em um livro, por exemplo) encontrar a derivada na forma que você escreveu do que na forma exibida pelo programa.

[Cálculo: Limites, Derivadas e Integrais] - Derivação de quo

[Cálculo: Limites, Derivadas e Integrais] - Derivação de quo

[Cálculo: Limites, Derivadas e Integrais] - Derivação de quo

Re: [Cálculo: Limites, Derivadas e Integrais] - Derivação de

Re: [Cálculo: Limites, Derivadas e Integrais] - Derivação de

Re: [Cálculo: Limites, Derivadas e Integrais] - Derivação de

Quem está online