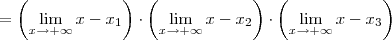por jr_freitas » Sex Out 07, 2011 16:55
por jr_freitas » Sex Out 07, 2011 16:55
Boa tarde!
Tenho dúvida no seguinte exercício: pede pra indicar nos problemas abaixo
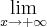
f(x) e

f(x) para cada função dada. Se o valor for infinito indique se é
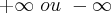
.

Usando a regra da potência maior, fiz assim:
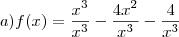
aí fazendo as contas deu f(x) = 1 -0 -0 que f(x)=1, não sei se essa parte está certo ou se precisava fazer isso... como eu sei que o resultado vai pra +

ou -

ou os dois?
Obrigado!
Abraço
-
jr_freitas
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Qui Out 06, 2011 10:28
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Tecnólogo em Análise de Sistemas
- Andamento: cursando
 por Claudin » Sáb Out 08, 2011 12:59
por Claudin » Sáb Out 08, 2011 12:59
http://www.wolframalpha.com/input/?i=lim_{x-%3E%2B%5Cinfty}+x^3-4x^2-4
Não consegui compreender este exercício, eu utilizava a mesma técnica, mas parece que esta dando errado.
Quando posso utilizar a técnica de dividir por maior expoente e quando não posso?
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Renato_RJ » Sáb Out 08, 2011 13:10
por Renato_RJ » Sáb Out 08, 2011 13:10
Amigos, tudo em paz ??
Essa "técnica", na verdade, consiste em colocar o termo de maior grau em evidência e não dividir o polinômio por ele, usamos essa técnica quando temos uma fração onde tanto o denominador quanto o numerador são polinômios, então colocamos o termo de maior grau em evidência para cancelarmos ele.
Quando temos um limite da forma está apresentado, uma função polinomial, aplicamos o valor direto no polinômio e estudamos o seu comportamento, veja:

Pois o termo

"cresce" mais rápido do que os outros, logo o polinômio todo tende para o infinito positivo, mas quando x tende ao
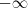
, o polinômio tende ao
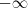
pois

mantém o sinal negativo...
Espero ter ajudado,
Renato.
Iniciando a minha "caminhada" pela matemática agora... Tenho muito o quê aprender...
-

Renato_RJ
- Colaborador Voluntário

-
- Mensagens: 306
- Registrado em: Qui Jan 06, 2011 15:47
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado em Matemática
- Andamento: cursando
 por Molina » Sáb Out 08, 2011 13:13
por Molina » Sáb Out 08, 2011 13:13
Boa tarde.
Pelo o que entendi vocês estão confundindo alguns conceitos. Esta técnica de dividir pelo maior expoente aplica-se quando eu tenho um quociente de duas funções, por exemplo:
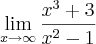
Neste caso sim divide pelo monômio dominante o numerador e o denominador.

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por Claudin » Sáb Out 08, 2011 18:37
por Claudin » Sáb Out 08, 2011 18:37
Correto, quando for operação quociente, posso utilizar a técnica de colocar em evidência?
E quando não for, procuro sempre multiplicar e dividir pelo conjugado?
Correto?
Então como resolver o exercício proposto no 1º post acima.
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por LuizAquino » Sáb Out 08, 2011 19:14
por LuizAquino » Sáb Out 08, 2011 19:14
Renato_RJ escreveu:(...)
Essa "técnica", na verdade, consiste em colocar o termo de maior grau em evidência e não dividir o polinômio por ele
(...)
Tanto faz enxergar a técnica como "colocar em evidência" ou como "dividir os polinômios."
Vamos tomar o exemplo:
 1) Método da "divisão"
1) Método da "divisão"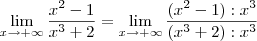

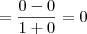 2) Método da "evidência"
2) Método da "evidência"

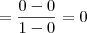
Obviamente, por qualquer um dos dois "métodos" a resposta é a mesma.
Claudin escreveu:Correto, quando for operação quociente, posso utilizar a técnica de colocar em evidência?
É por aí.
Claudin escreveu:E quando não for, procuro sempre multiplicar e dividir pelo conjugado?
Nem sempre.
Claudin escreveu:Então como resolver o exercício proposto no 1º post acima.
Desejamos resolver o limite:
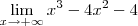
Do jeito que está, temos uma indeterminação do tipo

.
Aplicando os conhecimentos sobre os polinômios, sabemos que se

,

e
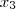
são as raízes do polinômio que aparece nesse limite, então podemos escrever que:

Não importa o valor das raízes, temos que o resultado desse último limite será:
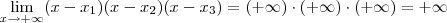
Portanto, temos que:

Se agora desejamos calcular esse limite quando
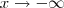
, então temos que:

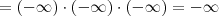
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Claudin » Sáb Out 08, 2011 19:22
por Claudin » Sáb Out 08, 2011 19:22
LuizAquino escreveu:Desejamos resolver o limite:
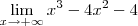
Do jeito que está, temos uma indeterminação do tipo

.
Aplicando os conhecimentos sobre os polinômios, sabemos que se

,

e
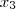
são as raízes do polinômio que aparece nesse limite, então podemos escrever que:

Não importa o valor das raízes, temos que o resultado desse último limite será:
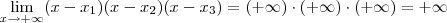
Portanto, temos que:

Se agora desejamos calcular esse limite quando
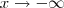
, então temos que:

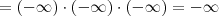
Correto, as explicações anteriores eu compreendi.
Mas esse método não compreendi como assim (x-x1)...?
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por LuizAquino » Sáb Out 08, 2011 19:35
por LuizAquino » Sáb Out 08, 2011 19:35
Claudin escreveu:Mas esse método não compreendi como assim (x-x1)...?
Para compreender as explicações dadas anteriormente é necessário que você saiba fatorar um polinômio.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Claudin » Sáb Out 08, 2011 19:38
por Claudin » Sáb Out 08, 2011 19:38
Claro que eu sei fatorar.
Se pudesse me explicar somente o x-x1...
ficarei grato
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por LuizAquino » Sáb Out 08, 2011 19:59
por LuizAquino » Sáb Out 08, 2011 19:59
Claudin escreveu:Claro que eu sei fatorar.
Se pudesse me explicar somente o x-x1...
ficarei grato
Se c é uma constante, então é válido que
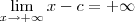
.
Desse modo, considerando que

,

e
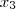
são constantes, será válido que
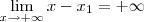
,
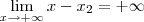
e

.
E agora, como você sabe fatorar, não deve enxergar problema algum em escrever o polinômio

como sendo igual a

, sendo

,

e
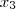
as raízes desse polinômio.
Portanto, no final temos que:

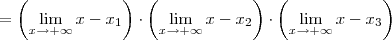

-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Claudin » Sáb Out 08, 2011 20:03
por Claudin » Sáb Out 08, 2011 20:03
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [limites no infinito]Limite no infinito de um ponto finito
por moyses » Ter Ago 30, 2011 12:45
- 3 Respostas
- 3528 Exibições
- Última mensagem por LuizAquino

Ter Ago 30, 2011 18:57
Cálculo: Limites, Derivadas e Integrais
-
- [Limites] Ajuda com limites no infinito e continuidade
 por umbrorz » Dom Abr 15, 2012 00:54
por umbrorz » Dom Abr 15, 2012 00:54
- 3 Respostas
- 4779 Exibições
- Última mensagem por umbrorz

Seg Abr 16, 2012 11:46
Cálculo: Limites, Derivadas e Integrais
-
- [LIMITES] Dúvida em questão de Limites no infinito
 por Jacques » Ter Jul 12, 2016 21:42
por Jacques » Ter Jul 12, 2016 21:42
- 4 Respostas
- 7549 Exibições
- Última mensagem por vitor_jo

Qua Jul 13, 2016 16:51
Cálculo: Limites, Derivadas e Integrais
-
- Limites no infinito
por felipe_ad » Sáb Abr 24, 2010 15:00
- 3 Respostas
- 5538 Exibições
- Última mensagem por MarceloFantini

Dom Abr 25, 2010 02:27
Cálculo: Limites, Derivadas e Integrais
-
- Limites no infinito
por Rosi7 » Sáb Mai 02, 2015 19:13
- 3 Respostas
- 2884 Exibições
- Última mensagem por DanielFerreira

Dom Mai 03, 2015 15:50
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 14 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
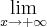 f(x) e
f(x) e  f(x) para cada função dada. Se o valor for infinito indique se é
f(x) para cada função dada. Se o valor for infinito indique se é 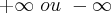 .
.
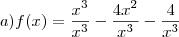 aí fazendo as contas deu f(x) = 1 -0 -0 que f(x)=1, não sei se essa parte está certo ou se precisava fazer isso... como eu sei que o resultado vai pra +
aí fazendo as contas deu f(x) = 1 -0 -0 que f(x)=1, não sei se essa parte está certo ou se precisava fazer isso... como eu sei que o resultado vai pra +  ou -
ou -  ou os dois?
ou os dois?



 "cresce" mais rápido do que os outros, logo o polinômio todo tende para o infinito positivo, mas quando x tende ao
"cresce" mais rápido do que os outros, logo o polinômio todo tende para o infinito positivo, mas quando x tende ao 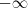 , o polinômio tende ao
, o polinômio tende ao 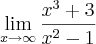



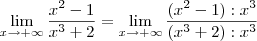



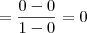
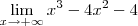
 .
. ,
,  e
e 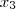 são as raízes do polinômio que aparece nesse limite, então podemos escrever que:
são as raízes do polinômio que aparece nesse limite, então podemos escrever que:
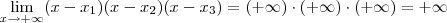

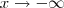 , então temos que:
, então temos que:
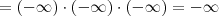
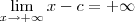 .
.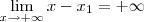 ,
, 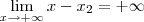 e
e  .
. como sendo igual a
como sendo igual a  , sendo
, sendo