Renato_RJ escreveu:(...)
Essa "técnica", na verdade, consiste em colocar o termo de maior grau em evidência e não dividir o polinômio por ele
(...)
Tanto faz enxergar a técnica como "colocar em evidência" ou como "dividir os polinômios."
Vamos tomar o exemplo:
 1) Método da "divisão"
1) Método da "divisão"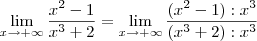

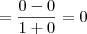 2) Método da "evidência"
2) Método da "evidência"

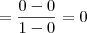
Obviamente, por qualquer um dos dois "métodos" a resposta é a mesma.
Claudin escreveu:Correto, quando for operação quociente, posso utilizar a técnica de colocar em evidência?
É por aí.
Claudin escreveu:E quando não for, procuro sempre multiplicar e dividir pelo conjugado?
Nem sempre.
Claudin escreveu:Então como resolver o exercício proposto no 1º post acima.
Desejamos resolver o limite:
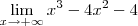
Do jeito que está, temos uma indeterminação do tipo

.
Aplicando os conhecimentos sobre os polinômios, sabemos que se

,

e
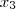
são as raízes do polinômio que aparece nesse limite, então podemos escrever que:

Não importa o valor das raízes, temos que o resultado desse último limite será:
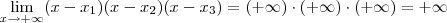
Portanto, temos que:

Se agora desejamos calcular esse limite quando
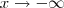
, então temos que:

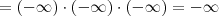
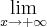 f(x) e
f(x) e  f(x) para cada função dada. Se o valor for infinito indique se é
f(x) para cada função dada. Se o valor for infinito indique se é 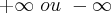 .
.
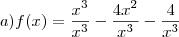 aí fazendo as contas deu f(x) = 1 -0 -0 que f(x)=1, não sei se essa parte está certo ou se precisava fazer isso... como eu sei que o resultado vai pra +
aí fazendo as contas deu f(x) = 1 -0 -0 que f(x)=1, não sei se essa parte está certo ou se precisava fazer isso... como eu sei que o resultado vai pra +  ou -
ou -  ou os dois?
ou os dois?



 "cresce" mais rápido do que os outros, logo o polinômio todo tende para o infinito positivo, mas quando x tende ao
"cresce" mais rápido do que os outros, logo o polinômio todo tende para o infinito positivo, mas quando x tende ao 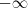 , o polinômio tende ao
, o polinômio tende ao 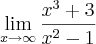



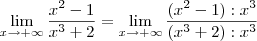



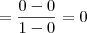
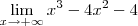
 .
. ,
,  e
e 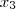 são as raízes do polinômio que aparece nesse limite, então podemos escrever que:
são as raízes do polinômio que aparece nesse limite, então podemos escrever que:
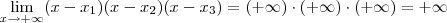

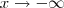 , então temos que:
, então temos que:
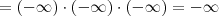
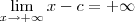 .
.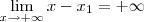 ,
, 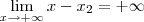 e
e  .
. como sendo igual a
como sendo igual a  , sendo
, sendo 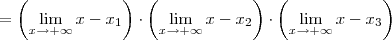


 , avisa que eu resolvo.
, avisa que eu resolvo.

