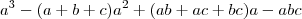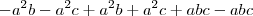por LuizCarlos » Seg Out 03, 2011 16:37
por LuizCarlos » Seg Out 03, 2011 16:37
Olá, estou tentando resolver uma expressão! mas não estou conseguindo!
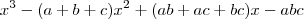
Não sei por onde começar!
-
LuizCarlos
- Colaborador Voluntário

-
- Mensagens: 254
- Registrado em: Ter Jun 21, 2011 20:39
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: 1º ano do segundo grau
- Andamento: cursando
 por futuro fisico » Seg Out 03, 2011 19:15
por futuro fisico » Seg Out 03, 2011 19:15
tua pergunta deve ta faltando dados, põe o contexto na qual a expressão esta inserida.Tipo coloca a questão.
No aguardo!
-
futuro fisico
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Sáb Jun 25, 2011 18:40
- Formação Escolar: GRADUAÇÃO
- Área/Curso: fisica medica
- Andamento: cursando
 por LuizCarlos » Seg Out 03, 2011 21:42
por LuizCarlos » Seg Out 03, 2011 21:42
È mesmo futuro fisíco, esqueci de colocar, que

obrigado desde ja pela ajuda.
-
LuizCarlos
- Colaborador Voluntário

-
- Mensagens: 254
- Registrado em: Ter Jun 21, 2011 20:39
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: 1º ano do segundo grau
- Andamento: cursando
 por joaofonseca » Ter Out 04, 2011 19:13
por joaofonseca » Ter Out 04, 2011 19:13
Depois de substituir x por a fica:
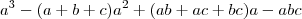
Começa por desembaraçar os parentises e tudo começa a fazer sentido.
-
joaofonseca
- Colaborador Voluntário

-
- Mensagens: 196
- Registrado em: Sáb Abr 30, 2011 12:25
- Localização: Lisboa
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por LuizCarlos » Qua Out 05, 2011 16:18
por LuizCarlos » Qua Out 05, 2011 16:18
Ola joaofonseca, sim isso eu sei, a minha duvida é a seguinte, perceba que tem
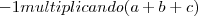
e também tem
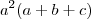
multiplicando.Quero saber por onde começar a multiplicação pelos termos ques estão dentro dos parenteses!
-
LuizCarlos
- Colaborador Voluntário

-
- Mensagens: 254
- Registrado em: Ter Jun 21, 2011 20:39
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: 1º ano do segundo grau
- Andamento: cursando
 por joaofonseca » Qua Out 05, 2011 18:57
por joaofonseca » Qua Out 05, 2011 18:57
Comecemos pelo inicio.
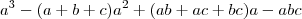
Sobre o primeiro parentesis existem duas operações.Basta executalas ao mesmo tempo.

Por observação, já se pode anular alguns termos.

Agora os outros parentesis
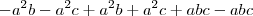
Se anularmos todos os termos simétricos ficamos com zero!
-
joaofonseca
- Colaborador Voluntário

-
- Mensagens: 196
- Registrado em: Sáb Abr 30, 2011 12:25
- Localização: Lisboa
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por LuizCarlos » Qui Out 06, 2011 16:43
por LuizCarlos » Qui Out 06, 2011 16:43
Entendi, obrigado joaofonseca!
Fazendo a propriedade distributiva da multiplicação em relação a soma algébrica, ficamos com termos simétricos, então é só anular! resultado zero!
obrigado, até!
-
LuizCarlos
- Colaborador Voluntário

-
- Mensagens: 254
- Registrado em: Ter Jun 21, 2011 20:39
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: 1º ano do segundo grau
- Andamento: cursando
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Ajuda em expressão!
por LuizCarlos » Qui Out 06, 2011 17:45
- 1 Respostas
- 557 Exibições
- Última mensagem por LuizCarlos

Qui Out 06, 2011 17:54
Álgebra Elementar
-
- Preciso de ajuda com uma expressão algébrica
por Lucas » Ter Ago 25, 2009 14:55
- 1 Respostas
- 1717 Exibições
- Última mensagem por tanialeite

Ter Ago 25, 2009 21:18
Álgebra Elementar
-
- Expressão , onde estou errando ? ajuda
por LuizCarlos » Qui Ago 04, 2011 23:37
- 8 Respostas
- 3218 Exibições
- Última mensagem por LuizCarlos

Sex Ago 05, 2011 01:40
Álgebra Elementar
-
- Expressão
por geriane » Qui Abr 22, 2010 12:49
- 4 Respostas
- 3885 Exibições
- Última mensagem por geriane

Sáb Abr 24, 2010 10:50
Trigonometria
-
- Expressão em PG
por Carolziiinhaaah » Qua Jun 16, 2010 21:10
- 1 Respostas
- 2006 Exibições
- Última mensagem por MarceloFantini

Qua Jun 16, 2010 21:39
Progressões
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
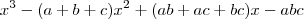

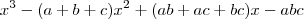




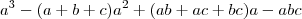

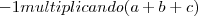 e também tem
e também tem 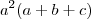 multiplicando.Quero saber por onde começar a multiplicação pelos termos ques estão dentro dos parenteses!
multiplicando.Quero saber por onde começar a multiplicação pelos termos ques estão dentro dos parenteses!