![\lim_{x\rightarrow\infty} \sqrt[m]{x} \lim_{x\rightarrow\infty} \sqrt[m]{x}](/latexrender/pictures/96ccfe9c58ac8b10b61bda3ddb4fe0ca.png)
Olá galera, sou novo por aqui...
Estou cursando Eng. de Controle e Automação no CEFET/RJ e estou com uma dúvida na questão acima.
Na minha tentativa, consegui isso:
![\lim_{x\rightarrow\infty} \sqrt[m]{x} = \infty \lim_{x\rightarrow\infty} \sqrt[m]{x} = \infty](/latexrender/pictures/f6d211e04c3327faebe3e4b67b8548fd.png)
![\sqrt[m]{\infty} = {\infty}^{\frac{1}{m}} = \infty \sqrt[m]{\infty} = {\infty}^{\frac{1}{m}} = \infty](/latexrender/pictures/8758d1c6f948dff942b640b60c430f30.png)
Mas temos que
 , então, pode-se dizer que
, então, pode-se dizer que ![\sqrt[m]{\infty} = \pm\infty \sqrt[m]{\infty} = \pm\infty](/latexrender/pictures/790541b29a7cc10d72b8cd63b6f871ed.png) (quando "m" for par) e
(quando "m" for par) e ![\sqrt[m]{\infty} = +\infty \sqrt[m]{\infty} = +\infty](/latexrender/pictures/4b27d58ded39f103940512d0f980bb31.png) (quando "m" for ímpar), certo?
(quando "m" for ímpar), certo?Então o limite também seguiria a regra acima?
Agradeço à todo, grande abraço.


![\lim_{x\rightarrow +\infty} \sqrt[m]{x} = +\infty \lim_{x\rightarrow +\infty} \sqrt[m]{x} = +\infty](/latexrender/pictures/a22a211595aac684f0d2cf85e11c63a8.png)
![\lim_{x\rightarrow -\infty} \sqrt[m]{x} = -\infty \lim_{x\rightarrow -\infty} \sqrt[m]{x} = -\infty](/latexrender/pictures/c4d24b1f1d59823c9251a582dee1bd8b.png)

![y = \sqrt[]{4} y = \sqrt[]{4}](/latexrender/pictures/b10fcd2a3dc2e11bf4e407907df9f9c8.png)

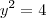

![y = \sqrt[]{\infty} y = \sqrt[]{\infty}](/latexrender/pictures/e1ff29b2740e10ba189ddf9ecb1fbc00.png)
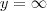

![y = \sqrt[]{}\infty y = \sqrt[]{}\infty](/latexrender/pictures/a134bf679462f0e7c393701c366061c9.png)
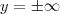


 , é um conceito, mas não um número fixo. Não faz sentido escrever algo como
, é um conceito, mas não um número fixo. Não faz sentido escrever algo como  . Quando você escreve algo desse tipo é como se você estivesse trabalhando com o conceito de infinito como se ele fosse um número qualquer fixo. O que podemos escrever (e faz sentido) seria algo como
. Quando você escreve algo desse tipo é como se você estivesse trabalhando com o conceito de infinito como se ele fosse um número qualquer fixo. O que podemos escrever (e faz sentido) seria algo como  .
.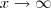 , sendo
, sendo 
![\lim_{x \to + \infty} \sqrt[m]{x} = + \infty \lim_{x \to + \infty} \sqrt[m]{x} = + \infty](/latexrender/pictures/899cc7d79e6b2753d9b1ea489a9b2b9f.png)
 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.