![\frac{dv}{dt}=\frac{3}{t \sqrt[]{t²-1}} \frac{dv}{dt}=\frac{3}{t \sqrt[]{t²-1}}](/latexrender/pictures/d5cc0c10e0da7530d669bbf7db7d9a2f.png) , t>1, v(2)=0
, t>1, v(2)=0Integrando cheguei a esse resultado:
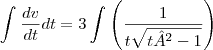
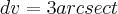
No livro, a resposta é
 ...
...De onde raios saiu esse

e não consegui tirar essa  de dentro da raiz tbm não rsrsrs... Alguem poderia me ajudar???

![\frac{dv}{dt}=\frac{3}{t \sqrt[]{t²-1}} \frac{dv}{dt}=\frac{3}{t \sqrt[]{t²-1}}](/latexrender/pictures/d5cc0c10e0da7530d669bbf7db7d9a2f.png) , t>1, v(2)=0
, t>1, v(2)=0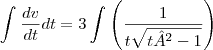
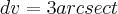
 ...
...

 , mas com a condição você encontra o valor de K.
, mas com a condição você encontra o valor de K.

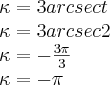
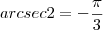 ...
...
 lê-se "o arco cuja secante é t", ou seja, você tem um ângulo
lê-se "o arco cuja secante é t", ou seja, você tem um ângulo  tal que
tal que 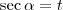 . Vamos ao exercício para facilitar o entendimento: se
. Vamos ao exercício para facilitar o entendimento: se  então
então  , mas
, mas 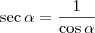 e daí
e daí  . O valor de
. O valor de  que satisfaz é
que satisfaz é  , e portanto
, e portanto 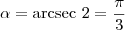 . Então, temos
. Então, temos 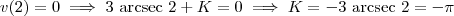 .
.


Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 4 visitantes
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)