 por mottasky » Ter Set 13, 2011 22:00
por mottasky » Ter Set 13, 2011 22:00
Galera, estou tentando resolver está Racionalização, mas estou meio perdido, se alguém puder me ajudar, a resposta eu sei gostaria de saber como resolver!
![Sendo \; A=\sqrt[3]{10-\sqrt[3]{6+\sqrt[3]{8}}} }\;e \; B= \sqrt[]{7 +\sqrt[]{7 - \sqrt[]{9}}}\,,calcule \,o \, valor \, de \; \sqrt[]{{A}^{4} + {B}^{2}} Sendo \; A=\sqrt[3]{10-\sqrt[3]{6+\sqrt[3]{8}}} }\;e \; B= \sqrt[]{7 +\sqrt[]{7 - \sqrt[]{9}}}\,,calcule \,o \, valor \, de \; \sqrt[]{{A}^{4} + {B}^{2}}](/latexrender/pictures/4b0688e99cb4639ac45922fc432edf6f.png)
Obs: o resultado tem que dar: 5
Obrigado pessoal!
-
mottasky
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Ter Set 13, 2011 21:20
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Informatica
- Andamento: formado
 por MarceloFantini » Ter Set 13, 2011 22:14
por MarceloFantini » Ter Set 13, 2011 22:14
Use que

e
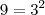
, isto cancelará as primeiras raízes. Daí tente enxergar o resto.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por mottasky » Qui Set 15, 2011 15:52
por mottasky » Qui Set 15, 2011 15:52
MarceloFantini escreveu:Use que

e
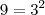
, isto cancelará as primeiras raízes. Daí tente enxergar o resto.
KKKKk
Muito obrigado, não acredito que não vi isso, a partir dai fica facil, é só ir cancelando muito obrigado!
-
mottasky
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Ter Set 13, 2011 21:20
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Informatica
- Andamento: formado
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Radiciação] Raiz dentro de raiz
por amandasousa_m » Sex Jul 19, 2013 09:37
- 2 Respostas
- 3438 Exibições
- Última mensagem por amandasousa_m

Sex Jul 19, 2013 21:58
Equações
-
- [raízes de números complexos] Raízes de uma equação com grau
por karenfreitas » Seg Ago 22, 2016 19:08
- 1 Respostas
- 8119 Exibições
- Última mensagem por adauto martins

Sáb Ago 27, 2016 16:11
Números Complexos
-
- Probabilidade dentro de uma matriz
por joaos92 » Ter Dez 14, 2010 15:29
- 3 Respostas
- 3407 Exibições
- Última mensagem por gichan

Qui Dez 16, 2010 12:21
Estatística
-
- Meter dentro da raiz
por seixas » Seg Ago 22, 2011 13:58
- 2 Respostas
- 2167 Exibições
- Última mensagem por seixas

Seg Ago 22, 2011 17:15
Polinômios
-
- Área dentro de um octógono
por anfran1 » Dom Ago 19, 2012 12:06
- 3 Respostas
- 2601 Exibições
- Última mensagem por anfran1

Dom Nov 17, 2013 10:34
Geometria Plana
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![Sendo \; A=\sqrt[3]{10-\sqrt[3]{6+\sqrt[3]{8}}} }\;e \; B= \sqrt[]{7 +\sqrt[]{7 - \sqrt[]{9}}}\,,calcule \,o \, valor \, de \; \sqrt[]{{A}^{4} + {B}^{2}} Sendo \; A=\sqrt[3]{10-\sqrt[3]{6+\sqrt[3]{8}}} }\;e \; B= \sqrt[]{7 +\sqrt[]{7 - \sqrt[]{9}}}\,,calcule \,o \, valor \, de \; \sqrt[]{{A}^{4} + {B}^{2}}](/latexrender/pictures/4b0688e99cb4639ac45922fc432edf6f.png)

![Sendo \; A=\sqrt[3]{10-\sqrt[3]{6+\sqrt[3]{8}}} }\;e \; B= \sqrt[]{7 +\sqrt[]{7 - \sqrt[]{9}}}\,,calcule \,o \, valor \, de \; \sqrt[]{{A}^{4} + {B}^{2}} Sendo \; A=\sqrt[3]{10-\sqrt[3]{6+\sqrt[3]{8}}} }\;e \; B= \sqrt[]{7 +\sqrt[]{7 - \sqrt[]{9}}}\,,calcule \,o \, valor \, de \; \sqrt[]{{A}^{4} + {B}^{2}}](/latexrender/pictures/4b0688e99cb4639ac45922fc432edf6f.png)

 e
e 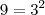 , isto cancelará as primeiras raízes. Daí tente enxergar o resto.
, isto cancelará as primeiras raízes. Daí tente enxergar o resto.

e
, isto cancelará as primeiras raízes. Daí tente enxergar o resto.

