![\lim_{x\rightarrow\infty}=\sqrt[]{x+2}-\sqrt[]{x} \lim_{x\rightarrow\infty}=\sqrt[]{x+2}-\sqrt[]{x}](/latexrender/pictures/fff8d9e41a8b08265504117c148b3367.png) a pergunta é a seguinte : um amigo aqui do forum o luiz me encinou que da para usar propriedades de potenciação para tirar tipos e indeterminaçoes como
a pergunta é a seguinte : um amigo aqui do forum o luiz me encinou que da para usar propriedades de potenciação para tirar tipos e indeterminaçoes como o problema é que esse exercicio cai numa indeterminação de
o problema é que esse exercicio cai numa indeterminação de  tem como usar as propriedades de potenciação nesse exercicio para tirar a indeterminação como esse que eu acabei de apresentar a vocês por favor me respondam:
tem como usar as propriedades de potenciação nesse exercicio para tirar a indeterminação como esse que eu acabei de apresentar a vocês por favor me respondam:Ps:eu sei propriedade mais com raiz eu nunca fiz, se não for incomodo por favor me passe um link confiavel que tenha funçoes trigonometricas , logaritmos de base E, e tabem limites fundamentais trigonometricos e limites fundamentais esponencial se não for encomodo! desde já agradeço a atenção de todos valew pessoal




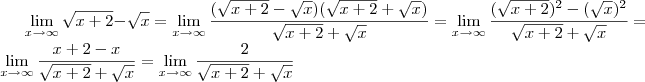
![\lim_{x\rightarrow\infty}\sqrt[]{x+2}-\sqrt[]{x} \lim_{x\rightarrow\infty}\sqrt[]{x+2}-\sqrt[]{x}](/latexrender/pictures/80d46f702b506210024f6cb24682ba2f.png) ai você pegou e multiplicou em cima e embaixa pro um mesmo valor só que o conjugado desse valor correto? ai quando você multiplicou esse por
ai você pegou e multiplicou em cima e embaixa pro um mesmo valor só que o conjugado desse valor correto? ai quando você multiplicou esse por ![\frac{\sqrt[]{x+2}+\sqrt[]{x}}{\sqrt[]{x+2}+\sqrt[]{x}} \frac{\sqrt[]{x+2}+\sqrt[]{x}}{\sqrt[]{x+2}+\sqrt[]{x}}](/latexrender/pictures/f79279af1f4011f2e49ee9b9b6a9df44.png) que não altera a fração , pois resultara no fração equivalente certo? ai você pegou e fez isso
que não altera a fração , pois resultara no fração equivalente certo? ai você pegou e fez isso ![\lim_{x\rightarrow\infty}\frac{\left(\sqrt[]{x+2}-\sqrt[]{x} \right)\left(\sqrt[]{x+2}+\sqrt[]{x} \right)}{1\left(\sqrt[]{x+2}+\sqrt[]{x} \right)} \lim_{x\rightarrow\infty}\frac{\left(\sqrt[]{x+2}-\sqrt[]{x} \right)\left(\sqrt[]{x+2}+\sqrt[]{x} \right)}{1\left(\sqrt[]{x+2}+\sqrt[]{x} \right)}](/latexrender/pictures/dcc93ff5392a1046de16813b89e7e313.png) que resulta nisso
que resulta nisso  :
: ![\lim_{x\rightarrow\infty}\frac{{\sqrt[]{x+2}}^{2}-{\sqrt[]{x}}^{2}}{1\left(\sqrt[]{x+2}+\sqrt[]{x} \right)} \lim_{x\rightarrow\infty}\frac{{\sqrt[]{x+2}}^{2}-{\sqrt[]{x}}^{2}}{1\left(\sqrt[]{x+2}+\sqrt[]{x} \right)}](/latexrender/pictures/c00c3bbaa8abd0ffc94223792d8f3b9a.png) depois fica assim ne?
depois fica assim ne? ![\lim_{x\rightarrow\infty}\frac{x+2-x}{\sqrt[]{x+2}+\sqrt[]{x}} \lim_{x\rightarrow\infty}\frac{x+2-x}{\sqrt[]{x+2}+\sqrt[]{x}}](/latexrender/pictures/1ad1bc19ad8c1c273a293be2128e94dd.png) =
= ![\lim_{x\rightarrow\infty}\frac{2}{\sqrt[]{x+2}+\sqrt[]{x}} \lim_{x\rightarrow\infty}\frac{2}{\sqrt[]{x+2}+\sqrt[]{x}}](/latexrender/pictures/b4819d27bdeb6650e48231cca6582860.png) agora se eu resolver fica assim:
agora se eu resolver fica assim: ![\lim_{x\rightarrow\infty}\frac{2}{\sqrt[]{\infty+2}+\sqrt[]{\infty}} \lim_{x\rightarrow\infty}\frac{2}{\sqrt[]{\infty+2}+\sqrt[]{\infty}}](/latexrender/pictures/bc479ca20d5a363aeda0d63bcb3d7ad1.png) =
= ![\lim_{x\rightarrow\infty}\frac{2}{\sqrt[]{\infty}+\sqrt[]{\infty}} \lim_{x\rightarrow\infty}\frac{2}{\sqrt[]{\infty}+\sqrt[]{\infty}}](/latexrender/pictures/34192202a168afdfc191d2eb4b928027.png) =
= =
= 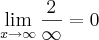 esse é eo resultado, se for se esclareça uma duvida? por qualquer numero não nulo sobre infinito vira 0? desde já valew pela ajuda ai no exercicio pessoal valeww
esse é eo resultado, se for se esclareça uma duvida? por qualquer numero não nulo sobre infinito vira 0? desde já valew pela ajuda ai no exercicio pessoal valeww 

 , onde K é uma constante, o limite será zero.
, onde K é uma constante, o limite será zero.

 que vai para zero, e portanto o limite inteiro vai para zero.
que vai para zero, e portanto o limite inteiro vai para zero. e
e 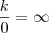 sera que eu estou certo? o infinito é um conceito de indeterminação ? mais quando dividimos k por 0 vai ser igual a +- infinito, é claro se os limites laterais forem iguais ai sim o limite que você fez ali no ponto esta correto!. quando dividimos k por 0 vai ser uma indeterminação , tentando entender sua explicação quando dividimos k por qualquer numero tentamos fazer que o denominador multiplicado por x numero , chegue ao k no numerador e o resultado é o numero que vc multiplica e chega no valor do denominador ! certo? mais qunado k e divido por 0 e k é dirente de 0 seja ele negativo ou positivo, então quantas vezes eu devo multiplicar 0 para chegar em k? não tem como pois 0 vezes qualquer coisa é sempre 0, por isso vai dar infinito pois eu ficarei infinitamente m,ultiplicando 0 para chegar a k é isso? e por isso o resultado via ser infinito?
sera que eu estou certo? o infinito é um conceito de indeterminação ? mais quando dividimos k por 0 vai ser igual a +- infinito, é claro se os limites laterais forem iguais ai sim o limite que você fez ali no ponto esta correto!. quando dividimos k por 0 vai ser uma indeterminação , tentando entender sua explicação quando dividimos k por qualquer numero tentamos fazer que o denominador multiplicado por x numero , chegue ao k no numerador e o resultado é o numero que vc multiplica e chega no valor do denominador ! certo? mais qunado k e divido por 0 e k é dirente de 0 seja ele negativo ou positivo, então quantas vezes eu devo multiplicar 0 para chegar em k? não tem como pois 0 vezes qualquer coisa é sempre 0, por isso vai dar infinito pois eu ficarei infinitamente m,ultiplicando 0 para chegar a k é isso? e por isso o resultado via ser infinito? , isso
, isso  no qual sabemos que
no qual sabemos que 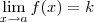 e
e 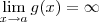 .
.