Gostaria que vocês me ajudassem em uma dúvida que eu estou tendo em vários exercícios. Talvez seja um erro de matemática simples (pra variar)...

Em uma das minhas listas de exercícios apareceu esta integral:
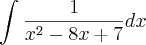
Bom, a minha resolução foi:
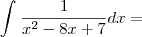
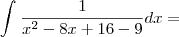
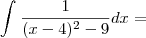
![\int_{}^{}\frac{1}{9[\frac{(x - 4)^2}{9} - 1]} dx = \int_{}^{}\frac{1}{9[\frac{(x - 4)^2}{9} - 1]} dx =](/latexrender/pictures/ad20545433c6e88b2551f1848635417c.png)
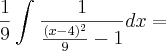
A partir deste ponto eu fiz a substituição para a variável
 (o exercício especificava que tinha que ser por substituição):
(o exercício especificava que tinha que ser por substituição):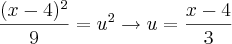
e consequentemente:
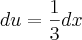
Até aí tudo bem. Eu substituí o
 e multipliquei a integral por três, por causa da fração que aparece no
e multipliquei a integral por três, por causa da fração que aparece no 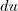 :
: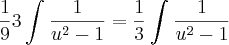
Acontece que eu coloquei essa integral no Wolfram e o resultado foi
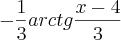
Acontece que o denominador da derivada da arctg é
 . Colocar um sinal negativo na constante que multiplica a integral faz com que esse sinal mude? Eu tive outras dúvidas desse tipo. Tiveram denominadores que, após a subatituição na variável
. Colocar um sinal negativo na constante que multiplica a integral faz com que esse sinal mude? Eu tive outras dúvidas desse tipo. Tiveram denominadores que, após a subatituição na variável  , apareceu
, apareceu  e no Wolfram tbm apareceu um resultado de
e no Wolfram tbm apareceu um resultado de 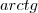 ... Pra mim só podia ser
... Pra mim só podia ser 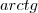 se aparecesse específicamente
se aparecesse específicamente  no denominador da integral.
no denominador da integral.Bom, se alguém puder esclarecer essa dúvida eu agradeço muito desde já

Obrigada e beijos!!!!!



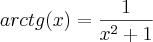
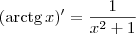
![\int \frac{1}{x^2 - 8x + 7}\, dx = \frac{1}{6}[\ln|x-7|-\ln|x-1|] + c \int \frac{1}{x^2 - 8x + 7}\, dx = \frac{1}{6}[\ln|x-7|-\ln|x-1|] + c](/latexrender/pictures/89ff78e2632e0e9dc9e3d13ae6d7a8d2.png)
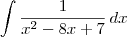
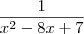 , complete the square:
, complete the square: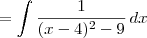
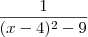 , substitute u = x-4 and du = dx:
, substitute u = x-4 and du = dx: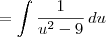
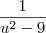 is
is 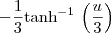 :
: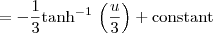
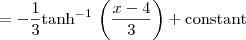
![= \frac{1}{6} [\log(7-x)-\log(1-x)]+\textrm{constant} = \frac{1}{6} [\log(7-x)-\log(1-x)]+\textrm{constant}](/latexrender/pictures/1fba74a20df5a1c2f8e2bfefdbaa516a.png)
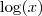 is the
is the 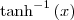 is the
is the 
 .
.



