Olha nao to conseguindo achar a resposta certa para esta questao.
![\int_{}^{}\frac{dx}{{x}^{2}\sqrt[2]{{x}^{2}-5}} \int_{}^{}\frac{dx}{{x}^{2}\sqrt[2]{{x}^{2}-5}}](/latexrender/pictures/48ee08596de5cbcca42cb76e03f543a8.png)
Bem eu fiz as devidas subsituiçoes, e resolvi como podem ver abaixo
substituiçoes:
![\sqrt[2]{{x}^{2}-5} = \sqrt[2]{5}.tg(\theta) \sqrt[2]{{x}^{2}-5} = \sqrt[2]{5}.tg(\theta)](/latexrender/pictures/96810cbb85747678feee797ea035b738.png)
![x = \sqrt[2]{5}.sec(\theta) x = \sqrt[2]{5}.sec(\theta)](/latexrender/pictures/8f8493f9b1418b2c23a1a2e8f6eda982.png)
![dx = \sqrt[2]{5}.sec(\theta).tg(\theta).d\theta dx = \sqrt[2]{5}.sec(\theta).tg(\theta).d\theta](/latexrender/pictures/a1bcc1436a25e2b7eb3a687b0db10d98.png)
Resoluçao:
![\int_{}^{}\frac{\sqrt[2]{5}.sec(\theta).tg(\theta).d\theta}{5.{sec}^{2}(\theta).\sqrt[2]{5}.tg(\theta)} \int_{}^{}\frac{\sqrt[2]{5}.sec(\theta).tg(\theta).d\theta}{5.{sec}^{2}(\theta).\sqrt[2]{5}.tg(\theta)}](/latexrender/pictures/a85c33ec8725dc819789c900fc86f421.png)

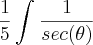

![\frac{1}{5}sen(\theta) = \frac{\sqrt[2]{{x}^{2}-5}}{5}+ C \frac{1}{5}sen(\theta) = \frac{\sqrt[2]{{x}^{2}-5}}{5}+ C](/latexrender/pictures/6fa255b9e28e5f709d80e5394c22a41b.png)
Resposta certa:
![\frac{\sqrt[2]{{x}^{2}-5}}{5x}+ C \frac{\sqrt[2]{{x}^{2}-5}}{5x}+ C](/latexrender/pictures/09a4f556903a3299fa9bd882b45e3f4f.png)
Ou seja, para resumir, da onde veio aquele x no denominador?





![\int_{}^{}\frac{dx}{{x}^{2}\sqrt[2]{{x}^{2}-5}} \int_{}^{}\frac{dx}{{x}^{2}\sqrt[2]{{x}^{2}-5}}](/latexrender/pictures/48ee08596de5cbcca42cb76e03f543a8.png)
![\sqrt[2]{{x}^{2}-5} = \sqrt[2]{5}.tg(\theta) \sqrt[2]{{x}^{2}-5} = \sqrt[2]{5}.tg(\theta)](/latexrender/pictures/96810cbb85747678feee797ea035b738.png)
![x = \sqrt[2]{5}.sec(\theta) x = \sqrt[2]{5}.sec(\theta)](/latexrender/pictures/8f8493f9b1418b2c23a1a2e8f6eda982.png)
![dx = \sqrt[2]{5}.sec(\theta).tg(\theta).d\theta dx = \sqrt[2]{5}.sec(\theta).tg(\theta).d\theta](/latexrender/pictures/a1bcc1436a25e2b7eb3a687b0db10d98.png)
![\int_{}^{}\frac{\sqrt[2]{5}.sec(\theta).tg(\theta).d\theta}{5.{sec}^{2}(\theta).\sqrt[2]{5}.tg(\theta)} \int_{}^{}\frac{\sqrt[2]{5}.sec(\theta).tg(\theta).d\theta}{5.{sec}^{2}(\theta).\sqrt[2]{5}.tg(\theta)}](/latexrender/pictures/a85c33ec8725dc819789c900fc86f421.png)

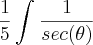

![\frac{1}{5}sen(\theta) = \frac{\sqrt[2]{{x}^{2}-5}}{5}+ C \frac{1}{5}sen(\theta) = \frac{\sqrt[2]{{x}^{2}-5}}{5}+ C](/latexrender/pictures/6fa255b9e28e5f709d80e5394c22a41b.png)
![\frac{\sqrt[2]{{x}^{2}-5}}{5x}+ C \frac{\sqrt[2]{{x}^{2}-5}}{5x}+ C](/latexrender/pictures/09a4f556903a3299fa9bd882b45e3f4f.png)





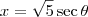 .
.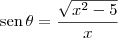 .
.

 )
)
paula luna escreveu:Desculpa os erros de portugues, ha um motivo significante para escolher a area da eng. (nao que isso explique os erros)

Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 5 visitantes
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)