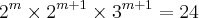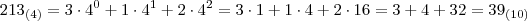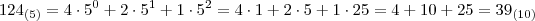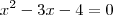por Gustavo R » Sáb Ago 13, 2011 18:05
por Gustavo R » Sáb Ago 13, 2011 18:05
1) Calcule m, sabendo-se que o número

admite 24 divisores naturais. r: m=2
pelos meus cálculos:
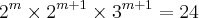
(m+1) (m+2) (m+2) = 24 É a partir daqui que eu tive várias dúvidas...
2) Um número natural se escreve 213 e 124 em duas bases distintas e consecutivas. Obtenha ese número no sistema decimal. r: 39
Nessa questão eu não consegui prosseguir...
Galera, se alguém souber, dá uma ajuda.. Obrigado e até mais!
-
Gustavo R
- Usuário Ativo

-
- Mensagens: 12
- Registrado em: Sex Ago 12, 2011 19:41
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Molina » Ter Ago 16, 2011 15:29
por Molina » Ter Ago 16, 2011 15:29
Boa tarde, Gustavo.
Gustavo R escreveu:1) Calcule m, sabendo-se que o número

admite 24 divisores naturais. r: m=2
pelos meus cálculos:
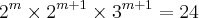
(m+1) (m+2) (m+2) = 24 É a partir daqui que eu tive várias dúvidas...
Você pode utilizar de um macete para não cair nesta equação de terceiro grau, veja:

Agora proceda como você havia feito e encontrará a resposta.
Qualquer dúvida, avise!

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por Gustavo R » Ter Ago 16, 2011 16:27
por Gustavo R » Ter Ago 16, 2011 16:27
entendi, Molina! obrigado! E se vc puder me dar uma força na questão 2, eu tmb agradeço. eu estou tendo dúvidas nela.Trata-se de sistemas de numeração.
Até mais!
-
Gustavo R
- Usuário Ativo

-
- Mensagens: 12
- Registrado em: Sex Ago 12, 2011 19:41
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Molina » Qua Ago 17, 2011 22:55
por Molina » Qua Ago 17, 2011 22:55
Boa noite, Gustavo.
Gustavo R escreveu:2) Um número natural se escreve 213 e 124 em duas bases distintas e consecutivas. Obtenha ese número no sistema decimal. r: 39
Eu pensei assim: se eles são de bases diferentes e consecutivas, significa que no 213 a base é 4 e no 124 a base é 5, já que num número na base
n o maior algarismo é
n-1. E fazendo isso vi que deu certo, veja:
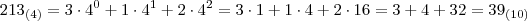
e
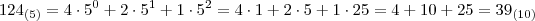
Legal a questão

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por Gustavo R » Sáb Ago 20, 2011 19:05
por Gustavo R » Sáb Ago 20, 2011 19:05
Molina escreveu:Boa noite, Gustavo.
Gustavo R escreveu:2) Um número natural se escreve 213 e 124 em duas bases distintas e consecutivas. Obtenha ese número no sistema decimal. r: 39
Eu pensei assim: se eles são de bases diferentes e consecutivas, significa que no 213 a base é 4 e no 124 a base é 5, já que num número na base
n o maior algarismo é
n-1. E fazendo isso vi que deu certo, veja:
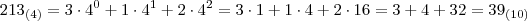
e
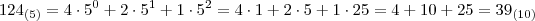
Legal a questão

td bem mas como se faz para chegar nessas duas bases sem saber q a resposta é 39? até mais!
-
Gustavo R
- Usuário Ativo

-
- Mensagens: 12
- Registrado em: Sex Ago 12, 2011 19:41
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Molina » Sáb Ago 20, 2011 19:16
por Molina » Sáb Ago 20, 2011 19:16
Revendo esta questão percebi que dava pra montar um sistema com ela, veja:
Seja x a base de 213 e (x+1) a base de 124. Lembre-se que elas são consecutivas:

Ajeitando isso aí de cima:

Como elas são iguais podemos igualá-las:

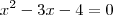
Cuja as raízes são 4 e -1. Como a base é positiva, eliminamos o -1 e ficamos apenas com o
4 (que é a base).

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por MarceloFantini » Sáb Ago 20, 2011 19:33
por MarceloFantini » Sáb Ago 20, 2011 19:33
Acredito que pelo sistema é a melhor forma, pois note que 23 escrito em base 7 é 32, porém nenhum dos seus algarimos é 6. Esta forma de raciocinar daria errado com este exemplo.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Molina » Sáb Ago 20, 2011 19:45
por Molina » Sáb Ago 20, 2011 19:45
MarceloFantini escreveu:Acredito que pelo sistema é a melhor forma, pois note que 23 escrito em base 7 é 32, porém nenhum dos seus algarimos é 6. Esta forma de raciocinar daria errado com este exemplo.
Sim, sim, sim. Percebi que meu chute deu certo por mera coincidência.

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- SISTEMAS DE NUMERAÇÃO
por metalll666 » Qua Jan 12, 2011 00:49
- 0 Respostas
- 1597 Exibições
- Última mensagem por metalll666

Qua Jan 12, 2011 00:49
Progressões
-
- [Sistemas de numeração] Achar bases diferentes
por armando » Seg Jun 20, 2016 15:06
- 1 Respostas
- 5062 Exibições
- Última mensagem por DanielFerreira

Sáb Jul 09, 2016 14:30
Teoria dos Números
-
- número de divisores ímpares
por thadeu » Dom Nov 22, 2009 23:23
- 0 Respostas
- 1142 Exibições
- Última mensagem por thadeu

Dom Nov 22, 2009 23:23
Álgebra Elementar
-
- Duvida - Quantas Divisores possíveis tem o numero N= 2 eleva
por rudson01 » Ter Abr 09, 2013 23:24
- 1 Respostas
- 1626 Exibições
- Última mensagem por DanielFerreira

Ter Abr 16, 2013 14:42
Probabilidade
-
- Numeração e Divisibilidade
por vanessaclm » Sáb Fev 25, 2012 14:36
- 1 Respostas
- 1774 Exibições
- Última mensagem por nathyn

Qui Mar 01, 2012 17:42
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 admite 24 divisores naturais. r: m=2
admite 24 divisores naturais. r: m=2