 por LuizCarlos » Dom Ago 14, 2011 16:48
por LuizCarlos » Dom Ago 14, 2011 16:48
-
LuizCarlos
- Colaborador Voluntário

-
- Mensagens: 254
- Registrado em: Ter Jun 21, 2011 20:39
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: 1º ano do segundo grau
- Andamento: cursando
 por Neperiano » Dom Ago 14, 2011 17:10
por Neperiano » Dom Ago 14, 2011 17:10
Ola
Cara tu ta sem complicando, não precisa igualar assim, faz por adição,é mais fácil pra ti, multiplica por 2 a equação debaixo.
Atenciosamente
Sómente os mortos conhecem o fim da guerra
"Platão"
-

Neperiano
- Colaborador Voluntário

-
- Mensagens: 960
- Registrado em: Seg Jun 16, 2008 17:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Produção
- Andamento: cursando
 por LuizCarlos » Dom Ago 14, 2011 17:47
por LuizCarlos » Dom Ago 14, 2011 17:47
Neperiano escreveu:Ola
Cara tu ta sem complicando, não precisa igualar assim, faz por adição,é mais fácil pra ti, multiplica por 2 a equação debaixo.
Atenciosamente
Ola Neperiano, mas o livro não ensina como você está falando, por adição !
Ele ensina por substituição e por comparação !
Como seria dessa forma que você está falando, e porque seria dessa forma, pois nao adianta eu saber fazer, e não saber o por que do que estou fazendo!
obrigado desde ja
-
LuizCarlos
- Colaborador Voluntário

-
- Mensagens: 254
- Registrado em: Ter Jun 21, 2011 20:39
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: 1º ano do segundo grau
- Andamento: cursando
 por LuizCarlos » Dom Ago 14, 2011 18:05
por LuizCarlos » Dom Ago 14, 2011 18:05
LuizCarlos escreveu:Neperiano escreveu:Ola
Cara tu ta sem complicando, não precisa igualar assim, faz por adição,é mais fácil pra ti, multiplica por 2 a equação debaixo.
Atenciosamente
Ola Neperiano, mas o livro não ensina como você está falando, por adição !
Ele ensina por substituição e por comparação !
Como seria dessa forma que você está falando, e porque seria dessa forma, pois nao adianta eu saber fazer, e não saber o por que do que estou fazendo!
obrigado desde ja
Neperiano, descobri todos meus erros, falta de atenção, realmente da forma que estava fazendo, estava me complicando!
Nesses casos o erro está aonde, eu deveria passar o 4 que está multiplicando o x, para o outro lado dividindo !
-
LuizCarlos
- Colaborador Voluntário

-
- Mensagens: 254
- Registrado em: Ter Jun 21, 2011 20:39
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: 1º ano do segundo grau
- Andamento: cursando
 por Neperiano » Dom Ago 14, 2011 18:10
por Neperiano » Dom Ago 14, 2011 18:10
Ola
Adição:
4x - 3y = - 2
-2x + 4y = 1 (x2)
4x-3y=-2
-4x +8y=2
0 + 5y =0
Logo y = 0
Substituindo na primeira
4x-3(0)=2
4x -0 = 2
x=1/2
Porque usar este jeito? Porque nele vocÊ nao precisa Isolar equações, só precisa pegar uma delas e multiplicar ou dividir por um valor, depois cortar a restrição (x ou y), eu acho mais fácil.
Mas cuidado nem sempre dá para usar este método.
Atenciosamente
Sómente os mortos conhecem o fim da guerra
"Platão"
-

Neperiano
- Colaborador Voluntário

-
- Mensagens: 960
- Registrado em: Seg Jun 16, 2008 17:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Produção
- Andamento: cursando
 por LuizCarlos » Dom Ago 14, 2011 18:58
por LuizCarlos » Dom Ago 14, 2011 18:58
Neperiano escreveu:Ola
Adição:
4x - 3y = - 2
-2x + 4y = 1 (x2)
4x-3y=-2
-4x +8y=2
0 + 5y =0
Logo y = 0
Substituindo na primeira
4x-3(0)=2
4x -0 = 2
x=1/2
Porque usar este jeito? Porque nele vocÊ nao precisa Isolar equações, só precisa pegar uma delas e multiplicar ou dividir por um valor, depois cortar a restrição (x ou y), eu acho mais fácil.
Mas cuidado nem sempre dá para usar este método.
Atenciosamente
Entendi amigo Neperiano, mas porque voce multiplicou a segundo equação por 2
somente nao entendi o por que multiplicar por 2, me explique fazendo favor
obrigado amigo
-
LuizCarlos
- Colaborador Voluntário

-
- Mensagens: 254
- Registrado em: Ter Jun 21, 2011 20:39
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: 1º ano do segundo grau
- Andamento: cursando
 por Neperiano » Dom Ago 14, 2011 19:01
por Neperiano » Dom Ago 14, 2011 19:01
Ola
Eu multiplique por 2 para poder cortar, eu vi que -2x2=-4 que cortava, mas não há uma logica você poderia ter dividido a primeira por 2, a ordem não importa, até porque quando vocÊ ver sistemas de equações com 4 incognitas, você precisara multilplicar muito, então sempre tenque ter atenção, para ver o que corta com o que.
Atenciosamente
Sómente os mortos conhecem o fim da guerra
"Platão"
-

Neperiano
- Colaborador Voluntário

-
- Mensagens: 960
- Registrado em: Seg Jun 16, 2008 17:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Produção
- Andamento: cursando
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Sistema Linear] MACK-SP: Sistema de Equações
por ALF » Sex Ago 26, 2011 13:24
- 1 Respostas
- 4502 Exibições
- Última mensagem por LuizAquino

Dom Ago 28, 2011 12:57
Sistemas de Equações
-
- Sistema de equações
por Cleyson007 » Sex Set 12, 2008 12:47
- 6 Respostas
- 5555 Exibições
- Última mensagem por Cleyson007

Qua Jun 03, 2009 17:25
Sistemas de Equações
-
- Sistema de Equações
por Cleyson007 » Qua Mai 27, 2009 14:01
- 3 Respostas
- 3352 Exibições
- Última mensagem por Cleyson007

Qui Mai 28, 2009 17:51
Sistemas de Equações
-
- Sistema de equações
por Moreno1986 » Seg Mai 17, 2010 15:04
- 3 Respostas
- 3600 Exibições
- Última mensagem por Neperiano

Ter Mai 18, 2010 17:54
Sistemas de Equações
-
- Sistema de equações
por Moreno1986 » Sex Abr 23, 2010 13:54
- 1 Respostas
- 1562 Exibições
- Última mensagem por MarceloFantini

Sáb Abr 24, 2010 00:56
Sistemas de Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 5 visitantes
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 10:38
Olá ! Tenho essa dúvida e não consigo montar o problema para resolução:
Qual é o racional não nulo cujo o quadrado é igual à sua terça parte ?
Grata.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 12:27

Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 12:55
também pensei que fosse assim, mas a resposta é

.
Obrigada Fantini.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 13:01

Como

:

O que você fez?
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 16:17
eu só consegui fazer a igualdade, não consegui desenvolver o restante, não pensei em fatoração, mas agora entendi o que vc fez.
Obrigada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
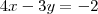
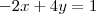
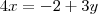













 .
.
 :
: