 por Pre-Universitario » Ter Ago 09, 2011 18:00
por Pre-Universitario » Ter Ago 09, 2011 18:00
Um rapaz observa o topo de um predio sob uma ngulo de 60 Graus.
Depois, se afasatando 100m vendo o predio sob um agulo agora de 30 Graus.
Qual a altura do predio.
Obs: a resposta ñ e em metros
Bom ! eu fiz e refiz essa questão varias veses mas ñ consegui achar o
resultado
quem poder fazer eu agradeço !
-
Pre-Universitario
- Usuário Ativo

-
- Mensagens: 22
- Registrado em: Sex Ago 05, 2011 17:16
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: 3
- Andamento: formado
 por LuizAquino » Ter Ago 09, 2011 19:34
por LuizAquino » Ter Ago 09, 2011 19:34
Esse exercício é análogo ao outro que você enviou no tópico:
[altura do prédio] A resposta esta correta ?viewtopic.php?f=109&t=5563Qual foi exatamente a sua dificuldade? Em que unidade de comprimento está exibida a resposta?
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Pre-Universitario » Qua Ago 10, 2011 15:41
por Pre-Universitario » Qua Ago 10, 2011 15:41
bom !
eu faço exatamente como o outro mas não consigo
achar essa resposta
![50\sqrt[]{3} 50\sqrt[]{3}](/latexrender/pictures/a83891c2a3a81fce40dac1276923bf36.png)
-
Pre-Universitario
- Usuário Ativo

-
- Mensagens: 22
- Registrado em: Sex Ago 05, 2011 17:16
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: 3
- Andamento: formado
 por LuizAquino » Qui Ago 11, 2011 19:39
por LuizAquino » Qui Ago 11, 2011 19:39
O exercício pode ser simplificado na figura abaixo. No caso, a altura do observador foi ignorada.
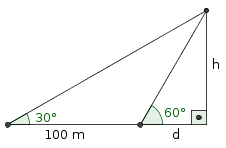
- altura_do_prédio.png (3.9 KiB) Exibido 1342 vezes
Podemos então escrever o sistema:
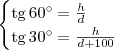
Isso é o mesmo que:

Da primeira equação, temos que

.
Podemos então reescrever a segunda equação como

. Resolvendo essa equação, obtemos

.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Trigonometria
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
zig - Sex Set 23, 2011 13:57
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
Vennom - Sex Set 23, 2011 21:41
zig escreveu:![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Rpz, o negócio é o seguinte:
Quando você tem uma potência negativa, tu deve inverter a base dela. Por exemplo:

Então pense o seguinte: a fração geratriz de 0,05 é

, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
Veja:
![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
A raiz quadrada de vinte, você acha fácil, né?
Espero ter ajudado.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:23
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:24
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



![50\sqrt[]{3} 50\sqrt[]{3}](/latexrender/pictures/a83891c2a3a81fce40dac1276923bf36.png)
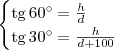

 .
. . Resolvendo essa equação, obtemos
. Resolvendo essa equação, obtemos  .
.![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.