 por LuizCarlos » Qua Ago 10, 2011 20:26
por LuizCarlos » Qua Ago 10, 2011 20:26
Comercei mas nao entendi, quando é numero eu consigo, só é envolver letra, complica !
Alguem poderia me ajudar como resolver o resto ? obrigado desde ja
- Anexos
-

-
LuizCarlos
- Colaborador Voluntário

-
- Mensagens: 254
- Registrado em: Ter Jun 21, 2011 20:39
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: 1º ano do segundo grau
- Andamento: cursando
 por Molina » Qua Ago 10, 2011 21:08
por Molina » Qua Ago 10, 2011 21:08
Boa noite.
Procure escrever suas mensagens no
e não simplesmente tirar uma foto da sua questão.
Você tem soma de frações em cima e embaixo. Vamos resolve-las separadamente:
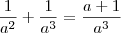
Faça o mesmo com as frações debaixo.
Em seguida você terá fração de frações, ou seja, no numerador você terá fração e no denominador você terá fração também. Caso não saiba como operar com isso, avise!

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por LuizCarlos » Qua Ago 10, 2011 21:32
por LuizCarlos » Qua Ago 10, 2011 21:32
Molina escreveu:Boa noite.
Procure escrever suas mensagens no
e não simplesmente tirar uma foto da sua questão.
Você tem soma de frações em cima e embaixo. Vamos resolve-las separadamente:
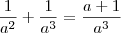
Faça o mesmo com as frações debaixo.
Em seguida você terá fração de frações, ou seja, no numerador você terá fração e no denominador você terá fração também. Caso não saiba como operar com isso, avise!

Ola amigo Diego, eu tirei foto, porque não sei usar esse LaTeX é muito complicado, não sei como fazer o risco de divisao usando esse LaTeX.
Gostaria que voce me explicasse por que ficou
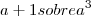
Quero entender por que ficou dessa forma, você faz o que? tira mmc , não estou entendendo!
-
LuizCarlos
- Colaborador Voluntário

-
- Mensagens: 254
- Registrado em: Ter Jun 21, 2011 20:39
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: 1º ano do segundo grau
- Andamento: cursando
 por Molina » Qua Ago 10, 2011 21:47
por Molina » Qua Ago 10, 2011 21:47
Boa noite.
Vamos por partes:

o mmc de

e
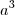
é
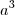
, por isso...
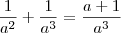
e
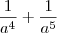
o mmc de
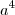
e

é

, por isso...

Ou seja, temos que:
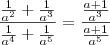
Agora você tem o que eu chamo de "fração de fração". Para resolver você vai repetir a fração de cima e MULTIPLICAR pelo INVERSO da fração de baixo:
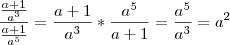

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por LuizCarlos » Qua Ago 10, 2011 22:15
por LuizCarlos » Qua Ago 10, 2011 22:15
Molina escreveu:Boa noite.
Vamos por partes:

o mmc de

e
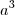
é
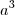
, por isso...
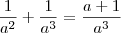
e

o mmc de
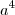
e

é

, por isso...

Ou seja, temos que:
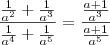
Agora você tem o que eu chamo de "fração de fração". Para resolver você vai repetir a fração de cima e MULTIPLICAR pelo INVERSO da fração de baixo:
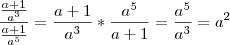

Ola Diego, boa noite, eu quero que vc me explique como você tirou o mmc, a minha duvida é somente nessa parte de tirar o mmc, eu não consigo tirar mmc com letras, e quando tem letra elevado a expoente, ae que fico confuso ainda mais! Se você me explicar como tirar o mmc detalhadamente, eu resolvo o resto.
Obrigado desde ja
-
LuizCarlos
- Colaborador Voluntário

-
- Mensagens: 254
- Registrado em: Ter Jun 21, 2011 20:39
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: 1º ano do segundo grau
- Andamento: cursando
 por Molina » Qua Ago 10, 2011 22:21
por Molina » Qua Ago 10, 2011 22:21
Boa noite.
LuizCarlos escreveu:Molina escreveu:Boa noite.
Vamos por partes:

o mmc de

e
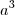
é
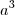
, por isso...
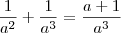
e

o mmc de
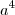
e

é

, por isso...

Ou seja, temos que:
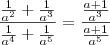
Agora você tem o que eu chamo de "fração de fração". Para resolver você vai repetir a fração de cima e MULTIPLICAR pelo INVERSO da fração de baixo:
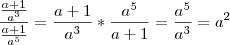

Ola Diego, boa noite, eu quero que vc me explique como você tirou o mmc, a minha duvida é somente nessa parte de tirar o mmc, eu não consigo tirar mmc com letras, e quando tem letra elevado a expoente, ae que fico confuso ainda mais! Se você me explicar como tirar o mmc detalhadamente, eu resolvo o resto.
Obrigado desde ja
O mmc entre letras iguais com expoentes, será sempre a com maior expoente. Veja porque:
Supor a = 2, teríamos que
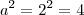
e
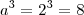
. O mmc(4,
8) =
8Supor a = 5, teríamos que
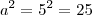
e
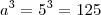
. O mmc(25,
125) =
125Supor a = 10, teríamos que
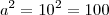
e
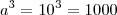
. O mmc(100,
1000) =
1000Generalizando,


Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por LuizCarlos » Qua Ago 10, 2011 22:46
por LuizCarlos » Qua Ago 10, 2011 22:46
Molina escreveu:Boa noite.
LuizCarlos escreveu:Molina escreveu:Boa noite.
Vamos por partes:

o mmc de

e
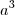
é
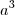
, por isso...
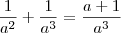
e

o mmc de
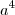
e

é

, por isso...

Ou seja, temos que:
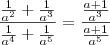
Agora você tem o que eu chamo de "fração de fração". Para resolver você vai repetir a fração de cima e MULTIPLICAR pelo INVERSO da fração de baixo:
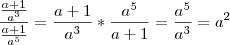

Ola Diego, boa noite, eu quero que vc me explique como você tirou o mmc, a minha duvida é somente nessa parte de tirar o mmc, eu não consigo tirar mmc com letras, e quando tem letra elevado a expoente, ae que fico confuso ainda mais! Se você me explicar como tirar o mmc detalhadamente, eu resolvo o resto.
Obrigado desde ja
O mmc entre letras iguais com expoentes, será sempre a com maior expoente. Veja porque:
Supor a = 2, teríamos que
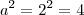
e
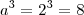
. O mmc(4,
8) =
8Supor a = 5, teríamos que
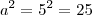
e
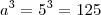
. O mmc(25,
125) =
125Supor a = 10, teríamos que
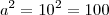
e
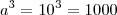
. O mmc(100,
1000) =
1000Generalizando,


agora entendi diego, mas no livro não encina, você ja viu algum que ensina mmc de letras elevadas a expoente númerico ?
-
LuizCarlos
- Colaborador Voluntário

-
- Mensagens: 254
- Registrado em: Ter Jun 21, 2011 20:39
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: 1º ano do segundo grau
- Andamento: cursando
 por LuizCarlos » Qua Ago 10, 2011 22:54
por LuizCarlos » Qua Ago 10, 2011 22:54
LuizCarlos escreveu:Molina escreveu:Boa noite.
LuizCarlos escreveu:Molina escreveu:Boa noite.
Vamos por partes:

o mmc de

e
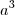
é
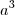
, por isso...
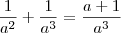
e

o mmc de
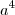
e

é

, por isso...

Ou seja, temos que:
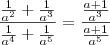
Agora você tem o que eu chamo de "fração de fração". Para resolver você vai repetir a fração de cima e MULTIPLICAR pelo INVERSO da fração de baixo:
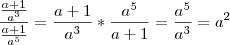

Ola Diego, boa noite, eu quero que vc me explique como você tirou o mmc, a minha duvida é somente nessa parte de tirar o mmc, eu não consigo tirar mmc com letras, e quando tem letra elevado a expoente, ae que fico confuso ainda mais! Se você me explicar como tirar o mmc detalhadamente, eu resolvo o resto.
Obrigado desde ja
O mmc entre letras iguais com expoentes, será sempre a com maior expoente. Veja porque:
Supor a = 2, teríamos que
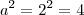
e
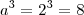
. O mmc(4,
8) =
8Supor a = 5, teríamos que
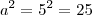
e
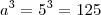
. O mmc(25,
125) =
125Supor a = 10, teríamos que
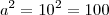
e
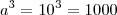
. O mmc(100,
1000) =
1000Generalizando,


agora entendi diego, mas no livro não encina, você ja viu algum que ensina mmc de letras elevadas a expoente númerico ?
Diego, e quando são letras diferentes, tipo nesse caso aqui ! como tiro o mmc, matematica parece que foi feito para complicar a mente do cara hehehehe
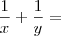
-
LuizCarlos
- Colaborador Voluntário

-
- Mensagens: 254
- Registrado em: Ter Jun 21, 2011 20:39
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: 1º ano do segundo grau
- Andamento: cursando
 por Molina » Qua Ago 10, 2011 23:01
por Molina » Qua Ago 10, 2011 23:01
Boa noite.
Neste caso, como
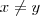
e não sabemos os seus valores, podemos considerar
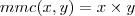
Logo,
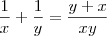

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por LuizCarlos » Qua Ago 10, 2011 23:07
por LuizCarlos » Qua Ago 10, 2011 23:07
Molina escreveu:Boa noite.
Neste caso, como
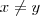
e não sabemos os seus valores, podemos considerar
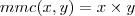
Logo,
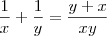

Hum entendi, então quando são letras diferentes, que não sabemos os valores, o mmc é as duas letras se multiplicando ? valeu amigo
-
LuizCarlos
- Colaborador Voluntário

-
- Mensagens: 254
- Registrado em: Ter Jun 21, 2011 20:39
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: 1º ano do segundo grau
- Andamento: cursando
 por LuizCarlos » Qua Ago 10, 2011 23:18
por LuizCarlos » Qua Ago 10, 2011 23:18
LuizCarlos escreveu:Molina escreveu:Boa noite.
Neste caso, como
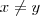
e não sabemos os seus valores, podemos considerar
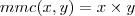
Logo,
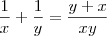

Hum entendi, então quando são letras diferentes, que não sabemos os valores, o mmc é as duas letras se multiplicando ? valeu amigo
Diego nesse caso aqui estou fazendo certo ?
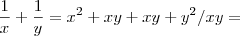

-
LuizCarlos
- Colaborador Voluntário

-
- Mensagens: 254
- Registrado em: Ter Jun 21, 2011 20:39
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: 1º ano do segundo grau
- Andamento: cursando
 por Molina » Qua Ago 10, 2011 23:22
por Molina » Qua Ago 10, 2011 23:22
LuizCarlos escreveu:LuizCarlos escreveu:Molina escreveu:Boa noite.
Neste caso, como
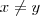
e não sabemos os seus valores, podemos considerar
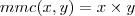
Logo,
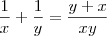

Hum entendi, então quando são letras diferentes, que não sabemos os valores, o mmc é as duas letras se multiplicando ? valeu amigo
Diego nesse caso aqui estou fazendo certo ?
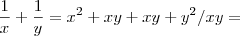

Não. Esta igualdade não é válida. Você deve estar se confundindo produtos notáveis.
Na verdade:
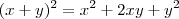
Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por LuizCarlos » Qua Ago 10, 2011 23:29
por LuizCarlos » Qua Ago 10, 2011 23:29
Molina escreveu:LuizCarlos escreveu:LuizCarlos escreveu:Molina escreveu:Boa noite.
Neste caso, como
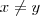
e não sabemos os seus valores, podemos considerar
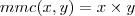
Logo,
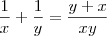

Hum entendi, então quando são letras diferentes, que não sabemos os valores, o mmc é as duas letras se multiplicando ? valeu amigo
Diego nesse caso aqui estou fazendo certo ?
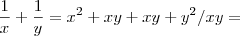

Não. Esta igualdade não é válida. Você deve estar se confundindo produtos notáveis.
Na verdade:
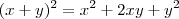
Não, eu tirei o mmc de
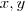
como fica nesse caso, quero comparar com o que eu fiz, mas nao consigo escrever em LaTex.
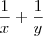
-
LuizCarlos
- Colaborador Voluntário

-
- Mensagens: 254
- Registrado em: Ter Jun 21, 2011 20:39
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: 1º ano do segundo grau
- Andamento: cursando
 por Molina » Qua Ago 10, 2011 23:36
por Molina » Qua Ago 10, 2011 23:36
Boa noite.
Eu já havia respondido isso:
Molina escreveu:Boa noite.
Neste caso, como
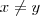
e não sabemos os seus valores, podemos considerar
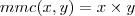
Logo,
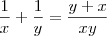

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por LuizCarlos » Qua Ago 10, 2011 23:42
por LuizCarlos » Qua Ago 10, 2011 23:42
Molina escreveu:Boa noite.
Eu já havia respondido isso:
Molina escreveu:Boa noite.
Neste caso, como
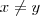
e não sabemos os seus valores, podemos considerar
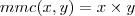
Logo,
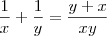

obrigado Diego, falta de atenção minha. Obrigado por tudo amigo
-
LuizCarlos
- Colaborador Voluntário

-
- Mensagens: 254
- Registrado em: Ter Jun 21, 2011 20:39
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: 1º ano do segundo grau
- Andamento: cursando
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- FUNÇOES nao estou entendendo!!
por joao1604 » Dom Fev 21, 2016 22:22
- 1 Respostas
- 1699 Exibições
- Última mensagem por DanielFerreira

Seg Fev 22, 2016 20:47
Funções
-
- Não estou entendendo esse problema!
por LuizCarlos » Sex Set 09, 2011 14:19
- 0 Respostas
- 1242 Exibições
- Última mensagem por LuizCarlos

Sex Set 09, 2011 14:19
Álgebra Elementar
-
- Problema de equação, não estou entendendo!
por LuizCarlos » Seg Dez 12, 2011 17:28
- 2 Respostas
- 2095 Exibições
- Última mensagem por TheoFerraz

Seg Dez 12, 2011 23:14
Álgebra Elementar
-
- Nao estou entendendo a questao e nao sei fazer la
por lukas keutzer » Ter Dez 13, 2011 17:00
- 1 Respostas
- 1652 Exibições
- Última mensagem por MarceloFantini

Ter Dez 13, 2011 21:08
Sistemas de Equações
-
- Não estou entendendo essa questão!!!
 por LuizCarlos » Qua Abr 11, 2012 16:50
por LuizCarlos » Qua Abr 11, 2012 16:50
- 2 Respostas
- 1788 Exibições
- Última mensagem por LuizCarlos

Qui Abr 12, 2012 14:51
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



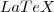 e não simplesmente tirar uma foto da sua questão.
e não simplesmente tirar uma foto da sua questão.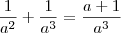


e não simplesmente tirar uma foto da sua questão.
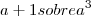


 e
e 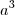 é
é 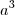 , por isso...
, por isso...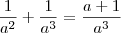

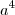 e
e  é
é  , por isso...
, por isso...
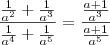
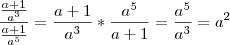


e
é
, por isso...
e
é
, por isso...

e
é
, por isso...
e
é
, por isso...
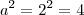 e
e 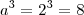 . O mmc(4,8) = 8
. O mmc(4,8) = 8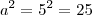 e
e 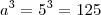 . O mmc(25,125) = 125
. O mmc(25,125) = 125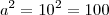 e
e 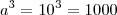 . O mmc(100,1000) = 1000
. O mmc(100,1000) = 1000


e
é
, por isso...
e
é
, por isso...
e
. O mmc(4,8) = 8
e
. O mmc(25,125) = 125
e
. O mmc(100,1000) = 1000

e
é
, por isso...
e
é
, por isso...
e
. O mmc(4,8) = 8
e
. O mmc(25,125) = 125
e
. O mmc(100,1000) = 1000
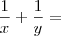

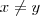 e não sabemos os seus valores, podemos considerar
e não sabemos os seus valores, podemos considerar 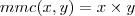
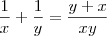


e não sabemos os seus valores, podemos considerar

e não sabemos os seus valores, podemos considerar
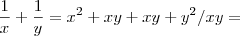


e não sabemos os seus valores, podemos considerar
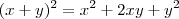

e não sabemos os seus valores, podemos considerar
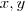
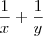

e não sabemos os seus valores, podemos considerar

e não sabemos os seus valores, podemos considerar
