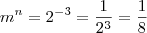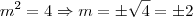Bom diga colegas.
Meu primeiro post aqui por sugestao de um amigo.
Atualmente estou estudando Redes e Comunicaçoes em Lima-Peru, por isso meu teclado nao acentua corretamente rss.
Como muitos de nós nao aprendemos suficiente na escola pública, principalmente para quem é egresso do Magistério, a situaçao é ainda pior.
Estou com dificuldades em resolver uma funçao, questao de prova. A funçao a seguir seria:
Dada a funçao: f= {(3,m^2); (2.5);(3.4);(2, n^2-4)}; Encontre m e n tal que (m – n) seja máxima. Dar como resposta m^n
O que está com o sinal ^ quer dizer elevado ao.
Sinceramente, nao entendi como resolver e aparentemente a funçao nao está bem formulada.
Lendo a resposta do livro, m ^2 = 4 e pela lógica n^2-4 = 5
Como posso resolver isso, ou ao menos, entender essa funçao?
Desde já agradeço.




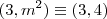



 :
: