 por EribertoTorres » Qua Ago 10, 2011 02:47
por EribertoTorres » Qua Ago 10, 2011 02:47
Bom diga colegas.
Meu primeiro post aqui por sugestao de um amigo.
Atualmente estou estudando Redes e Comunicaçoes em Lima-Peru, por isso meu teclado nao acentua corretamente rss.
Como muitos de nós nao aprendemos suficiente na escola pública, principalmente para quem é egresso do Magistério, a situaçao é ainda pior.
Estou com dificuldades em resolver uma funçao, questao de prova. A funçao a seguir seria:
Dada a funçao: f= {(3,m^2); (2.5);(3.4);(2, n^2-4)}; Encontre m e n tal que (m – n) seja máxima. Dar como resposta m^n
O que está com o sinal ^ quer dizer elevado ao.
Sinceramente, nao entendi como resolver e aparentemente a funçao nao está bem formulada.
Lendo a resposta do livro, m ^2 = 4 e pela lógica n^2-4 = 5
Como posso resolver isso, ou ao menos, entender essa funçao?
Desde já agradeço.
-
EribertoTorres
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Qua Ago 10, 2011 02:37
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Redes e Comunicaçoes
- Andamento: cursando
 por Molina » Qua Ago 10, 2011 13:39
por Molina » Qua Ago 10, 2011 13:39
Boa tarde, Eriberto.
Primeiramente seja bem-vindo!
Desculpe-me, mas não entendi sua função.
EribertoTorres escreveu:Dada a funçao: f= {(3,m^2); (2.5);(3.4);(2, n^2-4)};
Talvez seja uma notação que não conheço, poderia ser mais específico?
Fico no aguardo para poder te ajudar.

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por EribertoTorres » Qua Ago 10, 2011 13:57
por EribertoTorres » Qua Ago 10, 2011 13:57
Molina escreveu:Boa tarde, Eriberto.
Primeiramente seja bem-vindo!
Desculpe-me, mas não entendi sua função.
EribertoTorres escreveu:Dada a funçao: f= {(3,m^2); (2.5);(3.4);(2, n^2-4)};
Talvez seja uma notação que não conheço, poderia ser mais específico?
Fico no aguardo para poder te ajudar.

Ai mora o problema, veio assim e pelo visto ninguém entende a notaçao :(
Eu tenho a página com a resposta escaneada, subo em algum lugar e posto o link?
Eu quero entender como se faz, mas pelo visto tá dificil rss.
-
EribertoTorres
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Qua Ago 10, 2011 02:37
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Redes e Comunicaçoes
- Andamento: cursando
 por Molina » Qua Ago 10, 2011 14:00
por Molina » Qua Ago 10, 2011 14:00
EribertoTorres escreveu:Molina escreveu:Boa tarde, Eriberto.
Primeiramente seja bem-vindo!
Desculpe-me, mas não entendi sua função.
EribertoTorres escreveu:Dada a funçao: f= {(3,m^2); (2.5);(3.4);(2, n^2-4)};
Talvez seja uma notação que não conheço, poderia ser mais específico?
Fico no aguardo para poder te ajudar.

Ai mora o problema, veio assim e pelo visto ninguém entende a notaçao :(
Eu tenho a página com a resposta escaneada, subo em algum lugar e posto o link?
Eu quero entender como se faz, mas pelo visto tá dificil rss.
Sim, faça isso...
Você pode anexar imagens diretamente quando estiver escrevendo seu post.
Abaixo de onde você escreve (e abaixo dos botões de
salvar,
prever e
enviar) há uma aba
Anexar arquivo.
Qualquer dúvida, avise!

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por EribertoTorres » Qua Ago 10, 2011 14:29
por EribertoTorres » Qua Ago 10, 2011 14:29
Tá em espanhol, mas acho que dá para entender.
Nao sei se é uma forma diferente de fazer ou resolver, mas a resposta que eles dao é assim como no anexo.
- Anexos
-

-
EribertoTorres
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Qua Ago 10, 2011 02:37
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Redes e Comunicaçoes
- Andamento: cursando
 por Molina » Qua Ago 10, 2011 15:03
por Molina » Qua Ago 10, 2011 15:03
Boa tarde.
Vendo a solução, eu percebi que há uma relação entre o primeiro e terceiro parênteses da função, e entre o segundo e quarto parênteses. Veja:
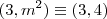

e


Para que (m-n) seja o maior possível, precisamos pegar o maior m (ou seja,
m'=2) e o menor n (ou seja,
n''=-3):
Aplicando o que o enunciado diz, temos que pegar esses valores em negrito e fazer
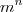
:
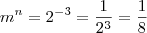
Qualquer dúvida, informe!

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por EribertoTorres » Qua Ago 10, 2011 15:16
por EribertoTorres » Qua Ago 10, 2011 15:16
Se eu entendi, uma vez que achei o valor de m e de n, eles podem ter 2 valores, tanto positivos, como negativos, correto?
Acho que ficou um pouco mais claro.
Uma dúvida, essa forma de notaçao é normal, comum, ou nao?
-
EribertoTorres
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Qua Ago 10, 2011 02:37
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Redes e Comunicaçoes
- Andamento: cursando
 por Molina » Qua Ago 10, 2011 15:20
por Molina » Qua Ago 10, 2011 15:20
EribertoTorres escreveu:Se eu entendi, uma vez que achei o valor de m e de n, eles podem ter 2 valores, tanto positivos, como negativos, correto?
Isso, eles podem ter dois valores, pois:
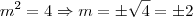
e

EribertoTorres escreveu:Uma dúvida, essa forma de notaçao é normal, comum, ou nao?
Sinceramente, não recordo de ter visto. Seria bom alguém do fórum que já tenha visto se manifestar.

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Dúvida em exerício. Função polinomial do primeiro grau.
por Danilo » Dom Mai 27, 2012 15:49
- 1 Respostas
- 3213 Exibições
- Última mensagem por DanielFerreira

Dom Mai 27, 2012 16:19
Funções
-
- +uma função das trevas.ajuda aew!(função par mas heim!?)
por Fabricio dalla » Dom Fev 27, 2011 16:12
- 2 Respostas
- 3488 Exibições
- Última mensagem por LuizAquino

Dom Mar 06, 2011 09:17
Funções
-
- Ajuda em Função!
por zekinha » Ter Jun 28, 2011 14:54
- 5 Respostas
- 3000 Exibições
- Última mensagem por MarceloFantini

Ter Jun 28, 2011 19:19
Funções
-
- [Função]Ajuda xD
por Giudav » Sex Abr 13, 2012 00:05
- 3 Respostas
- 2081 Exibições
- Última mensagem por DanielFerreira

Sex Abr 13, 2012 00:20
Funções
-
- Ajuda com função
por alan_lima » Ter Fev 21, 2017 16:53
- 0 Respostas
- 1951 Exibições
- Última mensagem por alan_lima

Ter Fev 21, 2017 16:53
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.




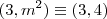



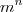 :
: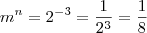
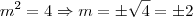

 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
