 por Claudin » Ter Ago 02, 2011 03:10
por Claudin » Ter Ago 02, 2011 03:10
Não consigo resolver este exercício de limite de função composta.
![\lim_{x\rightarrow1}\frac{\sqrt[3]{3x+5}-2}{x^2-1} \lim_{x\rightarrow1}\frac{\sqrt[3]{3x+5}-2}{x^2-1}](/latexrender/pictures/c5639b0a0ec0dd236176a49e0742a581.png)
Alguém poderia dar uma dica por onde começar?
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por FilipeCaceres » Ter Ago 02, 2011 09:17
por FilipeCaceres » Ter Ago 02, 2011 09:17
Olá Claudin,
Tente resolver conforme este
aquiAbraço.
-
FilipeCaceres
- Colaborador Voluntário

-
- Mensagens: 351
- Registrado em: Dom Out 31, 2010 21:43
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Tec. Mecatrônica
- Andamento: formado
 por Claudin » Ter Ago 02, 2011 16:07
por Claudin » Ter Ago 02, 2011 16:07
Já tentei de várias formas
Sendo:
![u=\sqrt[3]{3x+5} u=\sqrt[3]{3x+5}](/latexrender/pictures/283e5d88295698af82474b4f9433c690.png)
com
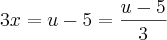
Tentei racionalizando também, mas não consegui.
Estou errando principalmente, pois no numerador seria 3x dentro da raiz, e no numerador seria um x², ai na hora de substituir os valores estou errando.
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por FilipeCaceres » Ter Ago 02, 2011 17:15
por FilipeCaceres » Ter Ago 02, 2011 17:15
Olá Claudin,
Uma forma seria reescrever da seguinte formar
![\lim_{x\rightarrow1}\frac{(\sqrt[3]{3x+5}-\sqrt[3]{8})}{x^2-1}.\frac{(\sqrt[3]{(3x+5)^2}+\sqrt[3]{3x+5}\sqrt[3]{8}+\sqrt[3]{8^2})}{(\sqrt[3]{(3x+5)^2}+\sqrt[3]{3x+5}\sqrt[3]{8}+\sqrt[3]{8^2})} \lim_{x\rightarrow1}\frac{(\sqrt[3]{3x+5}-\sqrt[3]{8})}{x^2-1}.\frac{(\sqrt[3]{(3x+5)^2}+\sqrt[3]{3x+5}\sqrt[3]{8}+\sqrt[3]{8^2})}{(\sqrt[3]{(3x+5)^2}+\sqrt[3]{3x+5}\sqrt[3]{8}+\sqrt[3]{8^2})}](/latexrender/pictures/8b3f5209cf758a1fcc69ec14a1ac5159.png)
Assim temos,
![\lim_{x\rightarrow1}\frac{3\cancel{(x-1)}}{\cancel{(x-1)}(x+1)(\sqrt[3]{(3x+5)^2}+2\sqrt[3]{3x+5}+4)} \lim_{x\rightarrow1}\frac{3\cancel{(x-1)}}{\cancel{(x-1)}(x+1)(\sqrt[3]{(3x+5)^2}+2\sqrt[3]{3x+5}+4)}](/latexrender/pictures/34b2b9530a240f73dc63c94c6661286d.png)
, pois

Logo,
![\lim_{x\rightarrow1}\frac{3}{(x+1)(\sqrt[3]{(3x+5)^2}+2\sqrt[3]{3x+5}+4)}=\frac{3}{2.(4+2.2+4)}=\frac{3}{2.12}=\boxed{\frac{1}{8}} \lim_{x\rightarrow1}\frac{3}{(x+1)(\sqrt[3]{(3x+5)^2}+2\sqrt[3]{3x+5}+4)}=\frac{3}{2.(4+2.2+4)}=\frac{3}{2.12}=\boxed{\frac{1}{8}}](/latexrender/pictures/c0a1117c399920bbeaf5e97f2264dfe5.png)
Abraço.
-
FilipeCaceres
- Colaborador Voluntário

-
- Mensagens: 351
- Registrado em: Dom Out 31, 2010 21:43
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Tec. Mecatrônica
- Andamento: formado
 por Claudin » Ter Ago 02, 2011 17:24
por Claudin » Ter Ago 02, 2011 17:24
Mas quando aplica-se a racionalização não era pra ficar assim?
![\lim_{x\rightarrow1}\frac{\sqrt[3]{3x+5}-2}{x^2-1}.\frac{\sqrt[3]{3x+5}+2}{\sqrt[3]{3x+5}+2} \lim_{x\rightarrow1}\frac{\sqrt[3]{3x+5}-2}{x^2-1}.\frac{\sqrt[3]{3x+5}+2}{\sqrt[3]{3x+5}+2}](/latexrender/pictures/90d2231393dbdf925fe07af9f0453206.png)
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por FilipeCaceres » Ter Ago 02, 2011 17:39
por FilipeCaceres » Ter Ago 02, 2011 17:39
Outra forma,
Temos,
![\lim_{x\rightarrow1}\frac{\sqrt[3]{3x+5}-2}{x^2-1} \lim_{x\rightarrow1}\frac{\sqrt[3]{3x+5}-2}{x^2-1}](/latexrender/pictures/c5639b0a0ec0dd236176a49e0742a581.png)
Façamos o seguinte
![u=\sqrt[3]{3x+5} u=\sqrt[3]{3x+5}](/latexrender/pictures/283e5d88295698af82474b4f9433c690.png)
,logo
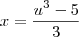
como

então
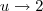
, pois
![u=\sqrt[3]{3.1+5}=2 u=\sqrt[3]{3.1+5}=2](/latexrender/pictures/2a0b1ebb88d71b7c22c1b7794c62b634.png)
Assim temos,
![\lim_{x\rightarrow1}\frac{\sqrt[3]{3x+5}-2}{x^2-1} \lim_{x\rightarrow1}\frac{\sqrt[3]{3x+5}-2}{x^2-1}](/latexrender/pictures/c5639b0a0ec0dd236176a49e0742a581.png)
![\lim_{x\rightarrow1}\frac{\sqrt[3]{3x+5}-2}{(x-1)(x+1)}=\lim_{u\rightarrow2}\frac{u-2}{(\frac{u^3-5}{3}-1)(\frac{u^3-5}{3}+1)} \lim_{x\rightarrow1}\frac{\sqrt[3]{3x+5}-2}{(x-1)(x+1)}=\lim_{u\rightarrow2}\frac{u-2}{(\frac{u^3-5}{3}-1)(\frac{u^3-5}{3}+1)}](/latexrender/pictures/552ecc8a3f528b14f26977ca528b7f25.png)
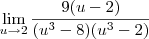
Fazendo,

Temos,
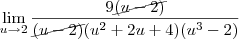
,pois


Mas quando aplica-se a racionalização não era pra ficar assim?
![\lim_{x\rightarrow1}\frac{\sqrt[3]{3x+5}-2}{x^2-1}.\frac{\sqrt[3]{3x+5}+2}{\sqrt[3]{3x+5}+2} \lim_{x\rightarrow1}\frac{\sqrt[3]{3x+5}-2}{x^2-1}.\frac{\sqrt[3]{3x+5}+2}{\sqrt[3]{3x+5}+2}](/latexrender/pictures/90d2231393dbdf925fe07af9f0453206.png)
Não.
Tente mostrar que:
![x-y=(\sqrt[3]{x}-\sqrt[3]{y})(\sqrt[3]{x^2}+\sqrt[3]{x.y}+\sqrt[3]{y^2}) x-y=(\sqrt[3]{x}-\sqrt[3]{y})(\sqrt[3]{x^2}+\sqrt[3]{x.y}+\sqrt[3]{y^2})](/latexrender/pictures/5a889a89fed7c380ac8eb40dc19c75e0.png)
Abraço.
-
FilipeCaceres
- Colaborador Voluntário

-
- Mensagens: 351
- Registrado em: Dom Out 31, 2010 21:43
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Tec. Mecatrônica
- Andamento: formado
 por Claudin » Ter Ago 02, 2011 18:06
por Claudin » Ter Ago 02, 2011 18:06
Você racionalizou aplicando o produto notável

. Somente, por ter uma raiz cúbica no exercício correto?
Se fosse uma raiz quadrada poderia racionalizar sem aplicação de produto notável, como fiz na ultima mensagem
deste tópico ?
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Claudin » Ter Ago 02, 2011 18:13
por Claudin » Ter Ago 02, 2011 18:13
FilipeCaceres escreveu:Outra forma,
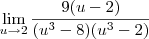
Não compreendi como apareceu este 9, no numerador.
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Limite] Gráfico e limite para função maior inteiro
 por Raphaela_sf » Qui Abr 05, 2012 19:26
por Raphaela_sf » Qui Abr 05, 2012 19:26
- 1 Respostas
- 6641 Exibições
- Última mensagem por LuizAquino

Qui Abr 05, 2012 20:53
Cálculo: Limites, Derivadas e Integrais
-
- [Limite] Limite de funções reais de várias variáveis
por Bianca_R » Dom Nov 04, 2012 17:17
- 1 Respostas
- 4786 Exibições
- Última mensagem por MarceloFantini

Dom Nov 04, 2012 19:37
Cálculo: Limites, Derivadas e Integrais
-
- [Limite trigonométrico] Como calculo este limite?
por Ronaldobb » Qua Nov 07, 2012 23:14
- 3 Respostas
- 5117 Exibições
- Última mensagem por Ronaldobb

Qui Nov 08, 2012 07:37
Cálculo: Limites, Derivadas e Integrais
-
- [Limite] limite trigonométrico quando x tende ao infinito
por Ge_dutra » Seg Jan 28, 2013 10:13
- 2 Respostas
- 7252 Exibições
- Última mensagem por Ge_dutra

Ter Jan 29, 2013 14:20
Cálculo: Limites, Derivadas e Integrais
-
- [Limite] Limite de funções piso (maior inteiro)
por ViniciusAlmeida » Sáb Fev 14, 2015 10:09
- 2 Respostas
- 4432 Exibições
- Última mensagem por adauto martins

Qui Fev 19, 2015 15:01
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 10:38
Olá ! Tenho essa dúvida e não consigo montar o problema para resolução:
Qual é o racional não nulo cujo o quadrado é igual à sua terça parte ?
Grata.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 12:27

Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 12:55
também pensei que fosse assim, mas a resposta é

.
Obrigada Fantini.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 13:01

Como

:

O que você fez?
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 16:17
eu só consegui fazer a igualdade, não consegui desenvolver o restante, não pensei em fatoração, mas agora entendi o que vc fez.
Obrigada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\lim_{x\rightarrow1}\frac{\sqrt[3]{3x+5}-2}{x^2-1} \lim_{x\rightarrow1}\frac{\sqrt[3]{3x+5}-2}{x^2-1}](/latexrender/pictures/c5639b0a0ec0dd236176a49e0742a581.png)

![\lim_{x\rightarrow1}\frac{\sqrt[3]{3x+5}-2}{x^2-1} \lim_{x\rightarrow1}\frac{\sqrt[3]{3x+5}-2}{x^2-1}](/latexrender/pictures/c5639b0a0ec0dd236176a49e0742a581.png)


![u=\sqrt[3]{3x+5} u=\sqrt[3]{3x+5}](/latexrender/pictures/283e5d88295698af82474b4f9433c690.png) com
com 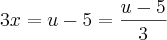

![\lim_{x\rightarrow1}\frac{(\sqrt[3]{3x+5}-\sqrt[3]{8})}{x^2-1}.\frac{(\sqrt[3]{(3x+5)^2}+\sqrt[3]{3x+5}\sqrt[3]{8}+\sqrt[3]{8^2})}{(\sqrt[3]{(3x+5)^2}+\sqrt[3]{3x+5}\sqrt[3]{8}+\sqrt[3]{8^2})} \lim_{x\rightarrow1}\frac{(\sqrt[3]{3x+5}-\sqrt[3]{8})}{x^2-1}.\frac{(\sqrt[3]{(3x+5)^2}+\sqrt[3]{3x+5}\sqrt[3]{8}+\sqrt[3]{8^2})}{(\sqrt[3]{(3x+5)^2}+\sqrt[3]{3x+5}\sqrt[3]{8}+\sqrt[3]{8^2})}](/latexrender/pictures/8b3f5209cf758a1fcc69ec14a1ac5159.png)
![\lim_{x\rightarrow1}\frac{3\cancel{(x-1)}}{\cancel{(x-1)}(x+1)(\sqrt[3]{(3x+5)^2}+2\sqrt[3]{3x+5}+4)} \lim_{x\rightarrow1}\frac{3\cancel{(x-1)}}{\cancel{(x-1)}(x+1)(\sqrt[3]{(3x+5)^2}+2\sqrt[3]{3x+5}+4)}](/latexrender/pictures/34b2b9530a240f73dc63c94c6661286d.png) , pois
, pois 
![\lim_{x\rightarrow1}\frac{3}{(x+1)(\sqrt[3]{(3x+5)^2}+2\sqrt[3]{3x+5}+4)}=\frac{3}{2.(4+2.2+4)}=\frac{3}{2.12}=\boxed{\frac{1}{8}} \lim_{x\rightarrow1}\frac{3}{(x+1)(\sqrt[3]{(3x+5)^2}+2\sqrt[3]{3x+5}+4)}=\frac{3}{2.(4+2.2+4)}=\frac{3}{2.12}=\boxed{\frac{1}{8}}](/latexrender/pictures/c0a1117c399920bbeaf5e97f2264dfe5.png)

![\lim_{x\rightarrow1}\frac{\sqrt[3]{3x+5}-2}{x^2-1}.\frac{\sqrt[3]{3x+5}+2}{\sqrt[3]{3x+5}+2} \lim_{x\rightarrow1}\frac{\sqrt[3]{3x+5}-2}{x^2-1}.\frac{\sqrt[3]{3x+5}+2}{\sqrt[3]{3x+5}+2}](/latexrender/pictures/90d2231393dbdf925fe07af9f0453206.png)

![\lim_{x\rightarrow1}\frac{\sqrt[3]{3x+5}-2}{x^2-1} \lim_{x\rightarrow1}\frac{\sqrt[3]{3x+5}-2}{x^2-1}](/latexrender/pictures/c5639b0a0ec0dd236176a49e0742a581.png)
![u=\sqrt[3]{3x+5} u=\sqrt[3]{3x+5}](/latexrender/pictures/283e5d88295698af82474b4f9433c690.png) ,logo
,logo 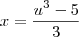 como
como  então
então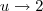 , pois
, pois ![u=\sqrt[3]{3.1+5}=2 u=\sqrt[3]{3.1+5}=2](/latexrender/pictures/2a0b1ebb88d71b7c22c1b7794c62b634.png)
![\lim_{x\rightarrow1}\frac{\sqrt[3]{3x+5}-2}{x^2-1} \lim_{x\rightarrow1}\frac{\sqrt[3]{3x+5}-2}{x^2-1}](/latexrender/pictures/c5639b0a0ec0dd236176a49e0742a581.png)
![\lim_{x\rightarrow1}\frac{\sqrt[3]{3x+5}-2}{(x-1)(x+1)}=\lim_{u\rightarrow2}\frac{u-2}{(\frac{u^3-5}{3}-1)(\frac{u^3-5}{3}+1)} \lim_{x\rightarrow1}\frac{\sqrt[3]{3x+5}-2}{(x-1)(x+1)}=\lim_{u\rightarrow2}\frac{u-2}{(\frac{u^3-5}{3}-1)(\frac{u^3-5}{3}+1)}](/latexrender/pictures/552ecc8a3f528b14f26977ca528b7f25.png)
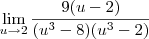

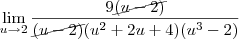 ,pois
,pois 

![x-y=(\sqrt[3]{x}-\sqrt[3]{y})(\sqrt[3]{x^2}+\sqrt[3]{x.y}+\sqrt[3]{y^2}) x-y=(\sqrt[3]{x}-\sqrt[3]{y})(\sqrt[3]{x^2}+\sqrt[3]{x.y}+\sqrt[3]{y^2})](/latexrender/pictures/5a889a89fed7c380ac8eb40dc19c75e0.png)

 . Somente, por ter uma raiz cúbica no exercício correto?
. Somente, por ter uma raiz cúbica no exercício correto?


 .
.
 :
: