 por Claudin » Qui Jul 28, 2011 17:08
por Claudin » Qui Jul 28, 2011 17:08
Livro Guidorizzi Vol 1
Página 85
Exercício 3
Dada a função

, verifique que

. Pergunta-se:
f é contínua em 1? Por Quê?
De acordo com meus cálculos encontrei

Ou seja, se os limites laterais pela esquerda e pela direita são iguais, determinei, que a função é contínua.
O que no gabarito esta dizendo o contrário.
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por LuizAquino » Qui Jul 28, 2011 18:37
por LuizAquino » Qui Jul 28, 2011 18:37
Claudin escreveu:De acordo com meus cálculos encontrei

Ou seja, se os limites laterais pela esquerda e pela direita são iguais, determinei, que a função é contínua.
Apenas ter limites laterais iguais quando x se aproxima de 1 não implica que a função seja contínua em 1. Basta você analisar a
definição de função contínua para entender isso.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Claudin » Qui Jul 28, 2011 19:49
por Claudin » Qui Jul 28, 2011 19:49
LuizAquino escreveu:Apenas ter limites laterais iguais quando x se aproxima de 1 não implica que a função seja contínua em 1. Basta você analisar a definição de função contínua para entender isso.
Então para ser uma função contínua teria que ser assim:
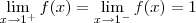
Correto?
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por LuizAquino » Qui Jul 28, 2011 20:27
por LuizAquino » Qui Jul 28, 2011 20:27
Claudin escreveu:Então para ser uma função contínua teria que ser assim:
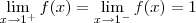
Correto?
Errado.
Conforme dito no outro tópico (
Limite), a função f é contínua em 1 se acontecer que:

-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Claudin » Qui Jul 28, 2011 21:06
por Claudin » Qui Jul 28, 2011 21:06
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Claudin » Sex Jul 29, 2011 02:04
por Claudin » Sex Jul 29, 2011 02:04
Analisando novamente o exercício Luiz Aquino, observei que na função:

Aplicando o
f(1) normalmente resultaria em uma indeterminação.
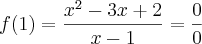
Mas o modo correto seria:
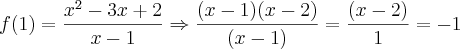
O que iria resultar em:
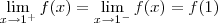
Substituindo valores:
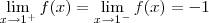
Após calcular os limites laterais pela esquerda e pela direita obtive:
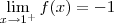
e

Ou seja, seria uma expressão correta, utilizando
f(1)=-1.
Poderia, explicar onde estou errando?
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Claudin » Sex Jul 29, 2011 02:08
por Claudin » Sex Jul 29, 2011 02:08
Com base nos cálculos acima posso afirmar que o limite existe.
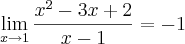
E automaticamente, com base nos cálculos acima, também pensei que a função seria contínua. Detalhe onde eu errei e explique-me a resposta correta. Obrigado.
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por LuizAquino » Sex Jul 29, 2011 09:29
por LuizAquino » Sex Jul 29, 2011 09:29
Claudin escreveu:(...)
Mas o modo correto seria:
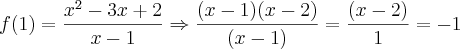
(...)
Poderia, explicar onde estou errando?
Exatamente nesse passo está o erro!
Só é possível simplificar os termos (x - 1) quando x for diferente de 1! Acontece que você simplificou esses termos e em seguida colocou x como 1.
Perceba que em outras palavras você está cometendo o
seguinte erro:

.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Claudin » Sex Jul 29, 2011 11:58
por Claudin » Sex Jul 29, 2011 11:58
Mas se não for desse modo. Aplicando
f(1) resultaria em uma indeterminação

Isso que eu não compreendi, por isso fiz desse modo.
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por LuizAquino » Sex Jul 29, 2011 12:16
por LuizAquino » Sex Jul 29, 2011 12:16
Claudin escreveu:Mas se não for desse modo. Aplicando
f(1) resultaria em uma indeterminação

Você
não pode calcular f(1), pois o domínio da função f é

.
Ou seja, x = 1
não faz parte do domínio de f. Desse modo, f(1)
não existe.
Essa função tem esse domínio devido a presença do termo (x - 1) no denominador.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Fabio Cabral » Sex Jul 29, 2011 12:20
por Fabio Cabral » Sex Jul 29, 2011 12:20
Claudinho,
Analisando o limite da função em x=1

Porém, não existe

Sabendo disso, já podemos afirmar que há uma descontinuidade!
" A Matemática não mente. Mente quem faz mau uso dela. " - Albert Einstein
-
Fabio Cabral
- Colaborador Voluntário

-
- Mensagens: 122
- Registrado em: Qua Out 06, 2010 11:33
- Localização: Brasília-DF
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Ciência da computação
- Andamento: cursando
 por Claudin » Sex Jul 29, 2011 12:23
por Claudin » Sex Jul 29, 2011 12:23
Compreendi Luiz e Fábio
Mas o fato de possuir limites laterais iguais não interfere na descontinuidade, certo?
Outra pergunta seria, então em questões de continuidade eu devo analisar primeiro se existe o ponto, certo?
Para depois analisar os limites laterais pela esquerda e pela direita?
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Fabio Cabral » Sex Jul 29, 2011 12:25
por Fabio Cabral » Sex Jul 29, 2011 12:25
" A Matemática não mente. Mente quem faz mau uso dela. " - Albert Einstein
-
Fabio Cabral
- Colaborador Voluntário

-
- Mensagens: 122
- Registrado em: Qua Out 06, 2010 11:33
- Localização: Brasília-DF
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Ciência da computação
- Andamento: cursando
 por Claudin » Sex Jul 29, 2011 12:27
por Claudin » Sex Jul 29, 2011 12:27
ok.

"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Fabio Cabral » Sex Jul 29, 2011 12:31
por Fabio Cabral » Sex Jul 29, 2011 12:31
Claudin escreveu:Compreendi Luiz e Fábio
Mas o fato de possuir limites laterais iguais não interfere na descontinuidade, certo?
Intefere. Se os limites laterais existirem e forem iguais, a função tera descontinuidade removível.
Caso contrário, será essencial!
" A Matemática não mente. Mente quem faz mau uso dela. " - Albert Einstein
-
Fabio Cabral
- Colaborador Voluntário

-
- Mensagens: 122
- Registrado em: Qua Out 06, 2010 11:33
- Localização: Brasília-DF
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Ciência da computação
- Andamento: cursando
 por Claudin » Sáb Jul 30, 2011 03:53
por Claudin » Sáb Jul 30, 2011 03:53
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Limite] Gráfico e limite para função maior inteiro
 por Raphaela_sf » Qui Abr 05, 2012 19:26
por Raphaela_sf » Qui Abr 05, 2012 19:26
- 1 Respostas
- 6641 Exibições
- Última mensagem por LuizAquino

Qui Abr 05, 2012 20:53
Cálculo: Limites, Derivadas e Integrais
-
- [Limite] Limite de funções reais de várias variáveis
por Bianca_R » Dom Nov 04, 2012 17:17
- 1 Respostas
- 4786 Exibições
- Última mensagem por MarceloFantini

Dom Nov 04, 2012 19:37
Cálculo: Limites, Derivadas e Integrais
-
- [Limite trigonométrico] Como calculo este limite?
por Ronaldobb » Qua Nov 07, 2012 23:14
- 3 Respostas
- 5117 Exibições
- Última mensagem por Ronaldobb

Qui Nov 08, 2012 07:37
Cálculo: Limites, Derivadas e Integrais
-
- [Limite] limite trigonométrico quando x tende ao infinito
por Ge_dutra » Seg Jan 28, 2013 10:13
- 2 Respostas
- 7251 Exibições
- Última mensagem por Ge_dutra

Ter Jan 29, 2013 14:20
Cálculo: Limites, Derivadas e Integrais
-
- [Limite] Limite de funções piso (maior inteiro)
por ViniciusAlmeida » Sáb Fev 14, 2015 10:09
- 2 Respostas
- 4432 Exibições
- Última mensagem por adauto martins

Qui Fev 19, 2015 15:01
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 , verifique que
, verifique que  . Pergunta-se: f é contínua em 1? Por Quê?
. Pergunta-se: f é contínua em 1? Por Quê?



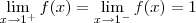


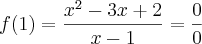
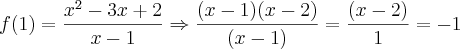
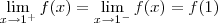
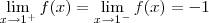
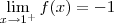 e
e 
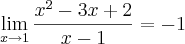
 .
.
 .
.

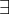



 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
