




 porque representa metade da área da figura geométrica plana?
porque representa metade da área da figura geométrica plana?
![\int_{0}^{1}x^2dx=\int_{0}^{1}[\frac{x^3}{3}]=\frac{1^3}{3}-\frac{0^3}{3}=\frac{1}{3} \int_{0}^{1}x^2dx=\int_{0}^{1}[\frac{x^3}{3}]=\frac{1^3}{3}-\frac{0^3}{3}=\frac{1}{3}](/latexrender/pictures/538921db209f46819ed52cb1e50d45e1.png)
![\int_{0}^{1}xdx=\int_{0}^{1}[\frac{x^2}{2}]=\frac{1^2}{2}-\frac{0^2}{2}=\frac{1}{2} \int_{0}^{1}xdx=\int_{0}^{1}[\frac{x^2}{2}]=\frac{1^2}{2}-\frac{0^2}{2}=\frac{1}{2}](/latexrender/pictures/cc6079b75c307df14664092f82fceb77.png)

Claudin escreveu:Como calcular uma integral?
Claudin escreveu:Como por exemplo aos 4:45 no vídeo 26 em que:
1º ex:
Claudin escreveu:2º exemplo que gostaria de deixar, seria o
O resultado só éporque representa metade da área da figura geométrica plana?
 representa a área entre o gráfico da função e o eixo x no intervalo [a, b].
representa a área entre o gráfico da função e o eixo x no intervalo [a, b].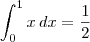 .
.
m0x0 escreveu:Para o 1º exemplo tens:
Para o 2º exemplo tens:
Espero ter ajudado.
![\int_{0}^{1}x^2\,dx\neq \int_{0}^{1}[\frac{x^3}{3}]\,dx \int_{0}^{1}x^2\,dx\neq \int_{0}^{1}[\frac{x^3}{3}]\,dx](/latexrender/pictures/863cd990b2915099d513cd20af2fefe3.png)
![\int_{0}^{1}x\,dx \neq \int_{0}^{1}[\frac{x^2}{2}]\,dx \int_{0}^{1}x\,dx \neq \int_{0}^{1}[\frac{x^2}{2}]\,dx](/latexrender/pictures/dfc0fdd836390fa915ac492ad7604d4a.png)
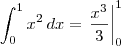
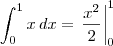

LuizAquino escreveu:Note que:
O que temos é:
Cuidado com as notações!
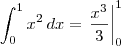
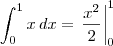

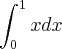

Claudin escreveu:LuizAquino escreveu:Note que:
O que temos é:
Cuidado com as notações!
Não consegui compreender como chegar em:
se o que temos a início seria:
Gostaria de saber detalhadamente como obter o cálculo da integral.
Obrigado Luiz e mOxO

 .
. é
é  .
. e perceba que você vai encontrar
e perceba que você vai encontrar  .
.



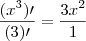

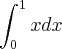
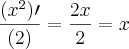


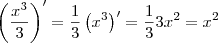



 e
e 


Claudin escreveu:Boa Noite Molina,
Agora sim compreendi.
Mas como chegar eme
Gostaria de saber qual próximo passo para ajudar a resolver uma integral.
Obrigado por ajudar a esclarecer a dúvida.
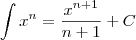
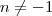

m0x0 escreveu:Para o 1º exemplo tens:
Para o 2º exemplo tens:
Espero ter ajudado.
 e
e 



Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 5 visitantes
 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :

