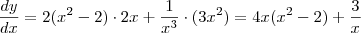por Kathleen » Dom Jun 26, 2011 19:20
por Kathleen » Dom Jun 26, 2011 19:20
Boa noite,
Vocês poderiam me ajudar nesta questão?
Y= (x²-2)² + Ln(x³)
Somente consegui resolver até:
y= 2(2x-2) + Ln (3x²)
y= 4(2x) + Ln (9x)
Grata!
-
Kathleen
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Dom Jun 26, 2011 19:06
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Administração de Empresas
- Andamento: cursando
 por Neperiano » Dom Jun 26, 2011 19:55
por Neperiano » Dom Jun 26, 2011 19:55
Ola
Não entendi muito bem o que queria, acho que é a derivada, então fica assim
y= x^4 - 4x^2 + 4 + Ln(x^3)
y' = 4x^3 - 8x + (3x^2)/x^3
Atenciosamente
Sómente os mortos conhecem o fim da guerra
"Platão"
-

Neperiano
- Colaborador Voluntário

-
- Mensagens: 960
- Registrado em: Seg Jun 16, 2008 17:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Produção
- Andamento: cursando
 por MarceloFantini » Dom Jun 26, 2011 20:11
por MarceloFantini » Dom Jun 26, 2011 20:11
Kathleen, qual é o enunciado da questão? Não sabemos o que você quer.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Kathleen » Dom Jun 26, 2011 21:28
por Kathleen » Dom Jun 26, 2011 21:28
Olá,
O enunciado é:
Calcule a seguinte derivada.
Grata!
-
Kathleen
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Dom Jun 26, 2011 19:06
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Administração de Empresas
- Andamento: cursando
 por MarceloFantini » Dom Jun 26, 2011 21:39
por MarceloFantini » Dom Jun 26, 2011 21:39
Bom, você tem duas regras da cadeia, devido a composição de funções, logo:
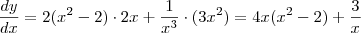
Foi meio rápido, quaisquer dúvidas pergunte.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Neperiano » Dom Jun 26, 2011 21:59
por Neperiano » Dom Jun 26, 2011 21:59
Ola
Só para esclarecer, as duas respostas estão certas a que eu derivei e a que o marcelo derivo, entretanto eu tirei do parenteses e não cortei o do Ln, mas de qualquer forma esta certa, mas o jeito do marcelo é mais prático, ele usa duas vezes a regra da cadeia, enquanto eu só usoi uma vez.
Atenciosamente
Sómente os mortos conhecem o fim da guerra
"Platão"
-

Neperiano
- Colaborador Voluntário

-
- Mensagens: 960
- Registrado em: Seg Jun 16, 2008 17:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Produção
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Derivada] Achar a derivada de uma função
por caiofisico » Seg Set 05, 2011 20:18
- 4 Respostas
- 3839 Exibições
- Última mensagem por caiofisico

Ter Set 06, 2011 19:44
Cálculo: Limites, Derivadas e Integrais
-
- [Derivada] Achar pontos de inflexão
por alienpuke » Qui Nov 12, 2015 11:31
- 2 Respostas
- 3769 Exibições
- Última mensagem por alienpuke

Ter Nov 17, 2015 10:01
Cálculo: Limites, Derivadas e Integrais
-
- Derivada: Achar os extremos da função(min/máx/inflexão)
por Fernandobertolaccini » Dom Jul 13, 2014 22:50
- 1 Respostas
- 1783 Exibições
- Última mensagem por e8group

Seg Jul 14, 2014 01:48
Cálculo: Limites, Derivadas e Integrais
-
- dificuldade em achar derivada(máximos e mínimos)
por letciabr7 » Qua Jun 10, 2015 17:51
- 1 Respostas
- 2196 Exibições
- Última mensagem por nakagumahissao

Sáb Jun 13, 2015 13:10
Cálculo: Limites, Derivadas e Integrais
-
- [DERIVADA] Duvida pra achar coeficiente angular
por Gatesco » Seg Jun 12, 2017 14:37
- 0 Respostas
- 3615 Exibições
- Última mensagem por Gatesco

Seg Jun 12, 2017 14:37
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 5 visitantes
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.