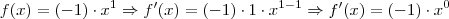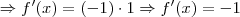por Isabela Sa » Qui Jun 23, 2011 12:34
por Isabela Sa » Qui Jun 23, 2011 12:34
Genteeee preciso de ajuda, se alguem me der explicação ficaria muito grata.
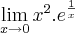
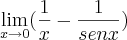
Coloquei "derivadas" mas é pq queria resolver por l'hospital
-
Isabela Sa
- Usuário Ativo

-
- Mensagens: 24
- Registrado em: Qui Jun 23, 2011 12:24
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Ensino Médio
- Andamento: cursando
 por MarceloFantini » Qui Jun 23, 2011 15:54
por MarceloFantini » Qui Jun 23, 2011 15:54
Quais são suas dúvidas e tentativas?
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Isabela Sa » Sex Jun 24, 2011 01:55
por Isabela Sa » Sex Jun 24, 2011 01:55
preciso q algm ajude a responder
pois eu n consigo por isso nao postei nada aki
minha duvida e simplismente como resolver por l'hopital esses casos.
obrigada
-
Isabela Sa
- Usuário Ativo

-
- Mensagens: 24
- Registrado em: Qui Jun 23, 2011 12:24
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Ensino Médio
- Andamento: cursando
 por MarceloFantini » Sex Jun 24, 2011 02:11
por MarceloFantini » Sex Jun 24, 2011 02:11
Transforme estes produtos numa divisão e então derive a função de cima, derive a debaixo e calcule o limite dessa nova divisão. Se continuar não existindo, repita o processo.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Molina » Sex Jun 24, 2011 02:36
por Molina » Sex Jun 24, 2011 02:36
Use a dica do Fantini.
Lembre-se que:
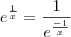
e que:
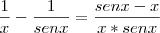

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por Isabela Sa » Sex Jun 24, 2011 02:44
por Isabela Sa » Sex Jun 24, 2011 02:44
se algum de vcs 2 pudesse resolver para mim
to quebrando a cabeça mas essa regra ta me matando to errando aki ainda
algm poste a soluço com os calculos POR FAVOR
obrigada
-
Isabela Sa
- Usuário Ativo

-
- Mensagens: 24
- Registrado em: Qui Jun 23, 2011 12:24
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Ensino Médio
- Andamento: cursando
 por MarceloFantini » Sex Jun 24, 2011 02:50
por MarceloFantini » Sex Jun 24, 2011 02:50
Isabela, mostre-nos seus cálculos e assim poderemos mostrar onde você está errando e assim você aprenderá melhor.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Isabela Sa » Sex Jun 24, 2011 11:08
por Isabela Sa » Sex Jun 24, 2011 11:08
Desisto!
Não consigo derivar isso
usa muito recurso algebrico
se algm puder me ajudar eu agradeço eternamente
mas eu queria a resolução!
Obrigada
-
Isabela Sa
- Usuário Ativo

-
- Mensagens: 24
- Registrado em: Qui Jun 23, 2011 12:24
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Ensino Médio
- Andamento: cursando
 por Fabio Cabral » Sex Jun 24, 2011 11:15
por Fabio Cabral » Sex Jun 24, 2011 11:15
Isabela, não há muito dificuldade em fazer isso.
Para aplicar L'Hopital, você precisa saber derivar.
Você sabe derivar?
Att,
" A Matemática não mente. Mente quem faz mau uso dela. " - Albert Einstein
-
Fabio Cabral
- Colaborador Voluntário

-
- Mensagens: 122
- Registrado em: Qua Out 06, 2010 11:33
- Localização: Brasília-DF
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Ciência da computação
- Andamento: cursando
 por Isabela Sa » Sex Jun 24, 2011 11:22
por Isabela Sa » Sex Jun 24, 2011 11:22
Sei sim Fábio
Voce poderia mostrar a resolução correta? ficaria mt grata
-
Isabela Sa
- Usuário Ativo

-
- Mensagens: 24
- Registrado em: Qui Jun 23, 2011 12:24
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Ensino Médio
- Andamento: cursando
 por Fabio Cabral » Sex Jun 24, 2011 12:08
por Fabio Cabral » Sex Jun 24, 2011 12:08
Vamos tomar como exemplo
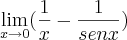
Como o Molina disse:

Logo, aplique a derivada tanto em cima quanto embaixo:
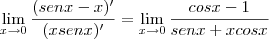
Veja que ainda teremos uma indeterminação do tipo

. Logo teremos que derivar novamente:
![\lim_{x\rightarrow0}\frac{(cosx-1)'}{(senx+xcosx)'}= \lim_{x\rightarrow0}\frac{-senx}{2cosx-xsenx} = \lim_{x\rightarrow0}\frac{-(0)}{2(1)-[(0).(0)]}= \lim_{x\rightarrow0}\frac{(cosx-1)'}{(senx+xcosx)'}= \lim_{x\rightarrow0}\frac{-senx}{2cosx-xsenx} = \lim_{x\rightarrow0}\frac{-(0)}{2(1)-[(0).(0)]}=](/latexrender/pictures/5c4b6a41d3733f09e54037c2d9430075.png)
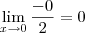
Caso tenha errado em algo, por favor, me corrijam.
" A Matemática não mente. Mente quem faz mau uso dela. " - Albert Einstein
-
Fabio Cabral
- Colaborador Voluntário

-
- Mensagens: 122
- Registrado em: Qua Out 06, 2010 11:33
- Localização: Brasília-DF
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Ciência da computação
- Andamento: cursando
 por Isabela Sa » Sex Jun 24, 2011 14:04
por Isabela Sa » Sex Jun 24, 2011 14:04
Eu so errei quando fui derivar senx -x = cosx ai eu n sabia q derivando "-x" iria ficar -1
outra coisa seria o xsenx = senx +xcosx eu achei q derivando xsenx ficaria xcosx
algm poderia explicar-me o porque?
e sobre o limite de e, algm me ajuda?
obrigada
-
Isabela Sa
- Usuário Ativo

-
- Mensagens: 24
- Registrado em: Qui Jun 23, 2011 12:24
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Ensino Médio
- Andamento: cursando
 por Molina » Sex Jun 24, 2011 14:14
por Molina » Sex Jun 24, 2011 14:14
Boa tarde, Isabela.
Isabela Sa escreveu:outra coisa seria o xsenx = senx +xcosx eu achei q derivando xsenx ficaria xcosx
Isso é a regra do produto. Lembre-se que:
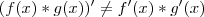
Ou seja, a derivada do produto é diferente do produto das derivadas.
Faça uma revisão deste assunto no seu material ou livro que está estudando. Há também uma outra regra para o quociente de derivadas.
Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por Fabio Cabral » Sex Jun 24, 2011 14:22
por Fabio Cabral » Sex Jun 24, 2011 14:22
Para derivar

você terá que aplicar a regra da Potência

ou seja:
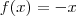
(veja que como o expoente não aparece, consideramos como 1, certo?) logo,
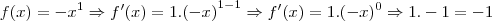
* Todo número elevado a 0 = 1.
" A Matemática não mente. Mente quem faz mau uso dela. " - Albert Einstein
-
Fabio Cabral
- Colaborador Voluntário

-
- Mensagens: 122
- Registrado em: Qua Out 06, 2010 11:33
- Localização: Brasília-DF
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Ciência da computação
- Andamento: cursando
 por Fabio Cabral » Sex Jun 24, 2011 14:31
por Fabio Cabral » Sex Jun 24, 2011 14:31
Isabela Sa escreveu:outra coisa seria o xsenx = senx +xcosx eu achei q derivando xsenx ficaria xcosx
Quanto à isso, como o Molina disse, aplique a Regra do Produto.
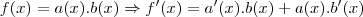
Logo:
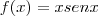
(Observe que, nesse caso, existe um produto entre x e senx, então use a regra do produto)
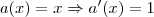

Agora, com base na Regra do produto:

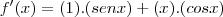

" A Matemática não mente. Mente quem faz mau uso dela. " - Albert Einstein
-
Fabio Cabral
- Colaborador Voluntário

-
- Mensagens: 122
- Registrado em: Qua Out 06, 2010 11:33
- Localização: Brasília-DF
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Ciência da computação
- Andamento: cursando
 por Isabela Sa » Sex Jun 24, 2011 15:31
por Isabela Sa » Sex Jun 24, 2011 15:31
Ate ai eu compreendi mas a confusao fica maior quando
tenho essa derivada f'(x)senx + xcosx
nao sei se fica (sen)'(x)+(sen)(x)'+ (x)'cosx+x(cos)' =
xcosx+senx + cosx-xsenx
Mas nao esta correto.
E sobre a "e" algm poderia me ajudar tbm?
obrigada
-
Isabela Sa
- Usuário Ativo

-
- Mensagens: 24
- Registrado em: Qui Jun 23, 2011 12:24
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Ensino Médio
- Andamento: cursando
 por Molina » Sex Jun 24, 2011 15:53
por Molina » Sex Jun 24, 2011 15:53
Boa tarde.
Para derivar isto

você só precisa fazer a regra do produto no segundo termo
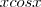
, veja:
![(senx + xcosx)' = (senx)' + (xcosx)' = cosx + [x*(-senx)+cosx*(1)]=2cosx-xsenx (senx + xcosx)' = (senx)' + (xcosx)' = cosx + [x*(-senx)+cosx*(1)]=2cosx-xsenx](/latexrender/pictures/f2b73d36b2b1a485fbeee84d5a1046ba.png)
Nos mostre o que você tem feito da primeira. Eu dei uma dica de como transformar aquele produto em um quociente. Use ele!
Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por Claudin » Sex Jun 24, 2011 17:34
por Claudin » Sex Jun 24, 2011 17:34
Vale lembrar Isabela que a regra de L'Hopital é utilizada quando há indeterminação do tipo

e

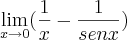
Tirando o mínimo e transformando em produto para facilitar os cálculos temos que:

Aplicando L'Hopital devido a indeterminação temos que:

Porém resultou em outra indeterminação devido a esse fato, aplique L'Hopital novamente, e claro vai cair na regra do produto, como foi explicado aqui em cima, vai resultar em:
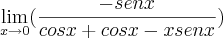
Com isso, resolvendo o limite normalmente temos que:
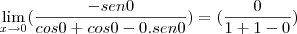
Portanto
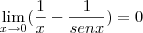
Espero ter especificado passo a passo para sanar sua dúvida, e sobre a outra questão tente pelo mesmo modo, qualquer coisa volte no tópico.
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Claudin » Sex Jun 24, 2011 17:46
por Claudin » Sex Jun 24, 2011 17:46
No exemplo que envolve "e" você também irá aplicar L'Hopital duas vezes e encontrará a resposta.

"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Isabela Sa » Sáb Jun 25, 2011 00:42
por Isabela Sa » Sáb Jun 25, 2011 00:42
fico mto agradecida pela explicaçao claudin
mas a do "e" eu n consegui resolver
-
Isabela Sa
- Usuário Ativo

-
- Mensagens: 24
- Registrado em: Qui Jun 23, 2011 12:24
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Ensino Médio
- Andamento: cursando
 por LuizAquino » Sáb Jun 25, 2011 22:58
por LuizAquino » Sáb Jun 25, 2011 22:58
Fabio Cabral escreveu:![\lim_{x\rightarrow0}\frac{(cosx-1)'}{(senx+xcosx)'}= \lim_{x\rightarrow0}\frac{-senx}{2cosx-xsenx} = \lim_{x\rightarrow0}\frac{-(0)}{2(1)-[(0).(0)]}= \lim_{x\rightarrow0}\frac{(cosx-1)'}{(senx+xcosx)'}= \lim_{x\rightarrow0}\frac{-senx}{2cosx-xsenx} = \lim_{x\rightarrow0}\frac{-(0)}{2(1)-[(0).(0)]}=](/latexrender/pictures/5c4b6a41d3733f09e54037c2d9430075.png)
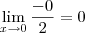
A partir do momento que você faz a aproximação de x por 2, não é mais necessário colocar o símbolo de limite.
Ou seja, basta escrever:
![\lim_{x\rightarrow 0}\frac{-\textrm{sen}\,x}{2\cos x-x\,\textrm{sen}\,x} = \frac{-(0)}{2(1)-[(0)\cdot (0)]}=\frac{-0}{2}=0 \lim_{x\rightarrow 0}\frac{-\textrm{sen}\,x}{2\cos x-x\,\textrm{sen}\,x} = \frac{-(0)}{2(1)-[(0)\cdot (0)]}=\frac{-0}{2}=0](/latexrender/pictures/3d422697d345a1cdb1212094969be3be.png)
Fabio Cabral escreveu:f(x)= -x (veja que como o expoente não aparece, consideramos como 1, certo?) logo,
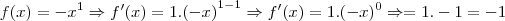
* Todo número elevado a 0 = 1.
Correção:
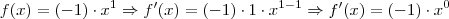
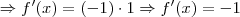
Além disso, vale destacar que:
"Todo número real
não nulo elevado a 0 é igual 1".
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Fabio Cabral » Ter Jun 28, 2011 00:15
por Fabio Cabral » Ter Jun 28, 2011 00:15
É, Luiz.
São coisas simples. Mas confesso a você que não dava importância a isso. Pra falar a verdade, é muito difícil encontrar um professor bem detalhista assim.
Bom, a gente aprende praticando e errando, certo? hehe
Obrigado mais uma vez!
" A Matemática não mente. Mente quem faz mau uso dela. " - Albert Einstein
-
Fabio Cabral
- Colaborador Voluntário

-
- Mensagens: 122
- Registrado em: Qua Out 06, 2010 11:33
- Localização: Brasília-DF
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Ciência da computação
- Andamento: cursando
 por LuizAquino » Ter Jun 28, 2011 09:38
por LuizAquino » Ter Jun 28, 2011 09:38
Fabio Cabral escreveu:É, Luiz.
São coisas simples. Mas confesso a você que não dava importância a isso.
Diz um provérbio chinês: só tropeçamos na pedra pequena, pois a grande nós desviamos.
É melhor você começar a dar importância aos "detalhes". Na sua área, por exemplo, um símbolo de "=" no lugar de "==" e um programa com milhares de linhas não vai funcionar direito! E detalhe: o compilador não vai avisar a você desse erro.
Fabio Cabral escreveu:Pra falar a verdade, é muito difícil encontrar um professor bem detalhista assim.
Bem, particularmente eu conheço vários! Inclusive, eu sou um deles.

Fabio Cabral escreveu:Bom, a gente aprende praticando e errando, certo? hehe
Com certeza!
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Fabio Cabral » Ter Jun 28, 2011 10:33
por Fabio Cabral » Ter Jun 28, 2011 10:33
LuizAquino escreveu:Fabio Cabral escreveu:É, Luiz.
São coisas simples. Mas confesso a você que não dava importância a isso.
Diz um provérbio chinês: só tropeçamos na pedra pequena, pois a grande nós desviamos.
É melhor você começar a dar importância aos "detalhes". Na sua área, por exemplo, um símbolo de "=" no lugar de "==" e um programa com milhares de linhas não vai funcionar direito! E detalhe: o compilador não vai avisar a você desse erro.
Fabio Cabral escreveu:Pra falar a verdade, é muito difícil encontrar um professor bem detalhista assim.
Bem, particularmente eu conheço vários! Inclusive, eu sou um deles.

Fabio Cabral escreveu:Bom, a gente aprende praticando e errando, certo? hehe
Com certeza!
É verdade. Trocar uma vírgula por um ponto ou vice-versa já é grave.
De qualquer forma, prestarei mais atenção.
 ps.:
ps.: Belo provérbio!
" A Matemática não mente. Mente quem faz mau uso dela. " - Albert Einstein
-
Fabio Cabral
- Colaborador Voluntário

-
- Mensagens: 122
- Registrado em: Qua Out 06, 2010 11:33
- Localização: Brasília-DF
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Ciência da computação
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Derivadas] Dificuldade para calcular derivadas CDI 1
por srmai » Seg Nov 04, 2013 01:21
- 0 Respostas
- 2260 Exibições
- Última mensagem por srmai

Seg Nov 04, 2013 01:21
Cálculo: Limites, Derivadas e Integrais
-
- [Derivadas] Interpretação de derivadas e funções
por vinik1 » Qua Out 12, 2011 16:03
- 5 Respostas
- 7465 Exibições
- Última mensagem por vinik1

Qui Out 13, 2011 10:48
Cálculo: Limites, Derivadas e Integrais
-
- [Derivadas] Derivadas em pontos dados
por MarlonMO250 » Sex Mar 01, 2013 21:02
- 6 Respostas
- 4938 Exibições
- Última mensagem por Russman

Sáb Mar 02, 2013 03:42
Cálculo: Limites, Derivadas e Integrais
-
- (derivadas) derivadas com raiz como se faz
por jana garcia » Qua Jun 25, 2014 00:28
- 1 Respostas
- 2960 Exibições
- Última mensagem por e8group

Qua Jun 25, 2014 01:13
Cálculo: Limites, Derivadas e Integrais
-
- [Derivadas] Derivadas com definição de limites
 por concurseironf » Sex Set 05, 2014 18:11
por concurseironf » Sex Set 05, 2014 18:11
- 1 Respostas
- 1988 Exibições
- Última mensagem por DanielFerreira

Dom Set 07, 2014 22:18
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
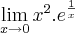
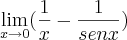

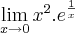
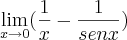





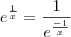
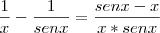








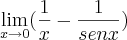

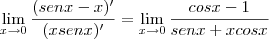
 . Logo teremos que derivar novamente:
. Logo teremos que derivar novamente:![\lim_{x\rightarrow0}\frac{(cosx-1)'}{(senx+xcosx)'}= \lim_{x\rightarrow0}\frac{-senx}{2cosx-xsenx} = \lim_{x\rightarrow0}\frac{-(0)}{2(1)-[(0).(0)]}= \lim_{x\rightarrow0}\frac{(cosx-1)'}{(senx+xcosx)'}= \lim_{x\rightarrow0}\frac{-senx}{2cosx-xsenx} = \lim_{x\rightarrow0}\frac{-(0)}{2(1)-[(0).(0)]}=](/latexrender/pictures/5c4b6a41d3733f09e54037c2d9430075.png)
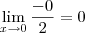


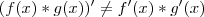

 você terá que aplicar a regra da Potência
você terá que aplicar a regra da Potência 
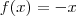 (veja que como o expoente não aparece, consideramos como 1, certo?) logo,
(veja que como o expoente não aparece, consideramos como 1, certo?) logo,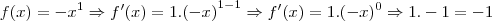

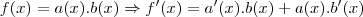 Logo:
Logo: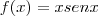 (Observe que, nesse caso, existe um produto entre x e senx, então use a regra do produto)
(Observe que, nesse caso, existe um produto entre x e senx, então use a regra do produto)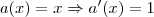


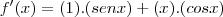



 você só precisa fazer a regra do produto no segundo termo
você só precisa fazer a regra do produto no segundo termo 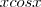 , veja:
, veja:![(senx + xcosx)' = (senx)' + (xcosx)' = cosx + [x*(-senx)+cosx*(1)]=2cosx-xsenx (senx + xcosx)' = (senx)' + (xcosx)' = cosx + [x*(-senx)+cosx*(1)]=2cosx-xsenx](/latexrender/pictures/f2b73d36b2b1a485fbeee84d5a1046ba.png)

 e
e 
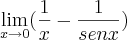


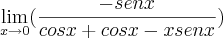
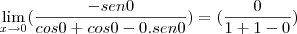
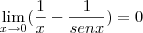




![\lim_{x\rightarrow 0}\frac{-\textrm{sen}\,x}{2\cos x-x\,\textrm{sen}\,x} = \frac{-(0)}{2(1)-[(0)\cdot (0)]}=\frac{-0}{2}=0 \lim_{x\rightarrow 0}\frac{-\textrm{sen}\,x}{2\cos x-x\,\textrm{sen}\,x} = \frac{-(0)}{2(1)-[(0)\cdot (0)]}=\frac{-0}{2}=0](/latexrender/pictures/3d422697d345a1cdb1212094969be3be.png)