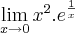
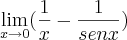
Coloquei "derivadas" mas é pq queria resolver por l'hospital

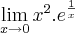
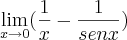





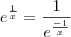








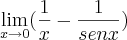

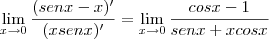
 . Logo teremos que derivar novamente:
. Logo teremos que derivar novamente:![\lim_{x\rightarrow0}\frac{(cosx-1)'}{(senx+xcosx)'}= \lim_{x\rightarrow0}\frac{-senx}{2cosx-xsenx} = \lim_{x\rightarrow0}\frac{-(0)}{2(1)-[(0).(0)]}= \lim_{x\rightarrow0}\frac{(cosx-1)'}{(senx+xcosx)'}= \lim_{x\rightarrow0}\frac{-senx}{2cosx-xsenx} = \lim_{x\rightarrow0}\frac{-(0)}{2(1)-[(0).(0)]}=](/latexrender/pictures/5c4b6a41d3733f09e54037c2d9430075.png)
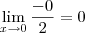


Isabela Sa escreveu:outra coisa seria o xsenx = senx +xcosx eu achei q derivando xsenx ficaria xcosx
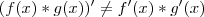

 você terá que aplicar a regra da Potência
você terá que aplicar a regra da Potência 
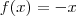 (veja que como o expoente não aparece, consideramos como 1, certo?) logo,
(veja que como o expoente não aparece, consideramos como 1, certo?) logo,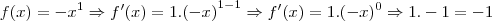

Isabela Sa escreveu:outra coisa seria o xsenx = senx +xcosx eu achei q derivando xsenx ficaria xcosx
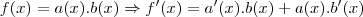 Logo:
Logo: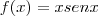 (Observe que, nesse caso, existe um produto entre x e senx, então use a regra do produto)
(Observe que, nesse caso, existe um produto entre x e senx, então use a regra do produto)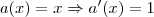


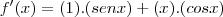



 você só precisa fazer a regra do produto no segundo termo
você só precisa fazer a regra do produto no segundo termo 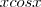 , veja:
, veja:![(senx + xcosx)' = (senx)' + (xcosx)' = cosx + [x*(-senx)+cosx*(1)]=2cosx-xsenx (senx + xcosx)' = (senx)' + (xcosx)' = cosx + [x*(-senx)+cosx*(1)]=2cosx-xsenx](/latexrender/pictures/f2b73d36b2b1a485fbeee84d5a1046ba.png)

 e
e 
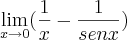


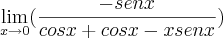
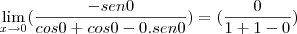
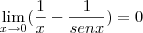




Fabio Cabral escreveu:
![\lim_{x\rightarrow 0}\frac{-\textrm{sen}\,x}{2\cos x-x\,\textrm{sen}\,x} = \frac{-(0)}{2(1)-[(0)\cdot (0)]}=\frac{-0}{2}=0 \lim_{x\rightarrow 0}\frac{-\textrm{sen}\,x}{2\cos x-x\,\textrm{sen}\,x} = \frac{-(0)}{2(1)-[(0)\cdot (0)]}=\frac{-0}{2}=0](/latexrender/pictures/3d422697d345a1cdb1212094969be3be.png)
Fabio Cabral escreveu:f(x)= -x (veja que como o expoente não aparece, consideramos como 1, certo?) logo,
* Todo número elevado a 0 = 1.
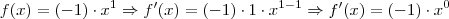
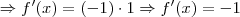


Fabio Cabral escreveu:É, Luiz.
São coisas simples. Mas confesso a você que não dava importância a isso.
Fabio Cabral escreveu:Pra falar a verdade, é muito difícil encontrar um professor bem detalhista assim.

Fabio Cabral escreveu:Bom, a gente aprende praticando e errando, certo? hehe

LuizAquino escreveu:Fabio Cabral escreveu:É, Luiz.
São coisas simples. Mas confesso a você que não dava importância a isso.
Diz um provérbio chinês: só tropeçamos na pedra pequena, pois a grande nós desviamos.
É melhor você começar a dar importância aos "detalhes". Na sua área, por exemplo, um símbolo de "=" no lugar de "==" e um programa com milhares de linhas não vai funcionar direito! E detalhe: o compilador não vai avisar a você desse erro.Fabio Cabral escreveu:Pra falar a verdade, é muito difícil encontrar um professor bem detalhista assim.
Bem, particularmente eu conheço vários! Inclusive, eu sou um deles.Fabio Cabral escreveu:Bom, a gente aprende praticando e errando, certo? hehe
Com certeza!


Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 8 visitantes
 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.