Ola
o problema é o seguinte
fazer o grafico de
f (x) =x³-3x²-9x
calculei a primeira derivada
f '(x) 3x²-6x-9
dps disso nao lembro mais
c alguem puder me dar dicas sobre o que fazer agradeço
obg






 e
e  . Quando você disse
. Quando você disse  eu pensei como se fosse o número decimal
eu pensei como se fosse o número decimal  . Agora lembre-se: depois de calcular a primeira derivada, verifique onde a função é crescente e decrescente vendo onde ela é positiva e onde ela é negativa. Em seguida, calcule a segunda derivada e ache os pontos de inflexão e onde ela é côncava ou convexa.
. Agora lembre-se: depois de calcular a primeira derivada, verifique onde a função é crescente e decrescente vendo onde ela é positiva e onde ela é negativa. Em seguida, calcule a segunda derivada e ache os pontos de inflexão e onde ela é côncava ou convexa.


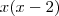 . Os pontos críticos são zero e dois. Agora resta analisar antes de zero, entre zero e dois e depois de dois. Antes de zero, esse produto é positivo, logo a função é positiva e crescente. Entre zero e dois, esse produto é negativo e portanto a função é decrescente(pois x é positivo porém x-2 é negativo). Depois de 2 volta a ser positivo e a função volta a ser crescente.
. Os pontos críticos são zero e dois. Agora resta analisar antes de zero, entre zero e dois e depois de dois. Antes de zero, esse produto é positivo, logo a função é positiva e crescente. Entre zero e dois, esse produto é negativo e portanto a função é decrescente(pois x é positivo porém x-2 é negativo). Depois de 2 volta a ser positivo e a função volta a ser crescente.

Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes

 .
.
 :
: