Exponencial - Dúvida 2

AjudaMatematica.com! Aqui você compartilha sua dúvida ou solução!

  • Anúncio Global
    Respostas
    Exibições
    Última mensagem

Exponencial - Dúvida 2

Regras do fórum
Responder

Exponencial - Dúvida 2

Mensagempor jamiel » Sáb Jun 18, 2011 22:02

\left(3*{5}^{{x}^{2}} + {3}^{{x}^{2}+1} - 8*{3}^{{x}^{2}} \right) \left(3*{5}^{{x}^{2}} + {3}^{{x}^{2}} * {3}^{1}} - 8*{3 }^{{x}^{2}}\right) \left(3*{5}^{{x}^{2}} - 5*{3}^{{x}^{2}} \right)


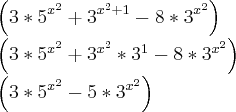
MInha dúvida é exatamente no fim, não sei se poderia fazer redução de termos. Pq se eu puder cortar um dos dois lados, o conjunto verdade seria V={±1}. Alguém para dar uma olhada?
jamiel
Colaborador Voluntário
Colaborador Voluntário
 
Mensagens: 131
Registrado em: Seg Jan 31, 2011 15:48
Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
Área/Curso: Mecânica
Andamento: cursando
Voltar ao topo

Re: Exponencial - Dúvida 2

Mensagempor MarceloFantini » Sáb Jun 18, 2011 22:17

Não há termos a reduzir, não tem termos em comum.
Futuro MATEMÁTICO
e^{\pi \cdot i} +1 = 0
MarceloFantini
Colaborador Moderador
Colaborador Moderador
 
Mensagens: 3126
Registrado em: Seg Dez 14, 2009 11:41
Formação Escolar: GRADUAÇÃO
Andamento: formado
Voltar ao topo

Re: Exponencial - Dúvida 2

Mensagempor jamiel » Sáb Jun 18, 2011 22:50

Será q aplicando log(x) resolverá?
jamiel
Colaborador Voluntário
Colaborador Voluntário
 
Mensagens: 131
Registrado em: Seg Jan 31, 2011 15:48
Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
Área/Curso: Mecânica
Andamento: cursando
Voltar ao topo

Re: Exponencial - Dúvida 2

Mensagempor MarceloFantini » Sáb Jun 18, 2011 22:53

Provavelmente.
Futuro MATEMÁTICO
e^{\pi \cdot i} +1 = 0
MarceloFantini
Colaborador Moderador
Colaborador Moderador
 
Mensagens: 3126
Registrado em: Seg Dez 14, 2009 11:41
Formação Escolar: GRADUAÇÃO
Andamento: formado
Voltar ao topo

Re: Exponencial - Dúvida 2

Mensagempor jamiel » Sáb Jun 18, 2011 23:02

vlw ....


rssr O pior é q quanto mais olho para isso, mais fico sem saber por onde começar!
jamiel
Colaborador Voluntário
Colaborador Voluntário
 
Mensagens: 131
Registrado em: Seg Jan 31, 2011 15:48
Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
Área/Curso: Mecânica
Andamento: cursando
Voltar ao topo

Re: Exponencial - Dúvida 2

Mensagempor MarceloFantini » Sáb Jun 18, 2011 23:14

Poste a questão na íntegra e poderemos te ajudar melhor.
Futuro MATEMÁTICO
e^{\pi \cdot i} +1 = 0
MarceloFantini
Colaborador Moderador
Colaborador Moderador
 
Mensagens: 3126
Registrado em: Seg Dez 14, 2009 11:41
Formação Escolar: GRADUAÇÃO
Andamento: formado
Voltar ao topo

Re: Exponencial - Dúvida 2

Mensagempor jamiel » Sáb Jun 18, 2011 23:20

A questão está na integra, mas o meu problema está na última parte. Eu não sei oq fazer para resolve-la!
jamiel
Colaborador Voluntário
Colaborador Voluntário
 
Mensagens: 131
Registrado em: Seg Jan 31, 2011 15:48
Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
Área/Curso: Mecânica
Andamento: cursando
Voltar ao topo

Re: Exponencial - Dúvida 2

Mensagempor MarceloFantini » Sáb Jun 18, 2011 23:31

Essa expressão não é igual a nada?
Futuro MATEMÁTICO
e^{\pi \cdot i} +1 = 0
MarceloFantini
Colaborador Moderador
Colaborador Moderador
 
Mensagens: 3126
Registrado em: Seg Dez 14, 2009 11:41
Formação Escolar: GRADUAÇÃO
Andamento: formado
Voltar ao topo

Re: Exponencial - Dúvida 2

Mensagempor jamiel » Dom Jun 19, 2011 00:13

Eu não estou conseguindo resolver a última, definitivamente. Sem contar, q eu posso ter errado antes em alguma parte!
jamiel
Colaborador Voluntário
Colaborador Voluntário
 
Mensagens: 131
Registrado em: Seg Jan 31, 2011 15:48
Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
Área/Curso: Mecânica
Andamento: cursando
Voltar ao topo
Responder

Voltar para Funções

 


Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!

  • Tópicos relacionados
    Respostas
    Exibições
    Última mensagem

Quem está online

Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante

 


Tópico Popular

Assunto: cálculo de limites
Autor: Hansegon - Seg Ago 25, 2008 11:29

Bom dia.

Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado

\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]

Assunto: cálculo de limites
Autor: Molina - Seg Ago 25, 2008 13:25

\lim_{x\rightarrow-1} \frac{{x}^{3}+1}{{x}^{2}-1}

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.

Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo. :y:

Caso ainda não tenha dado uma :idea:, avisa que eu resolvo.

Bom estudo!

Assunto: cálculo de limites
Autor: Guill - Dom Abr 08, 2012 16:03

\lim_{x\rightarrow-1}\frac{x^3+1}{x^2-1}

\lim_{x\rightarrow-1}\frac{(x+1)(x^2-x+1)}{(x+1)(x-1)}

\lim_{x\rightarrow-1}\frac{(x^2-x+1)}{(x-1)}=\frac{-3}{2}

Powered by phpBB © phpBB Group.

phpBB Mobile / SEO by Artodia.

Índice do fórum