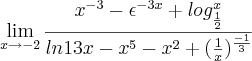
Não consegui chegar a resolução do exercício.
Quem puder ajudar, favor postar a resolução.
Obrigado
por Claudin » Sex Jun 03, 2011 15:31
por LuizAquino » Sex Jun 03, 2011 23:38
.
por Claudin » Seg Jun 06, 2011 17:08
por Claudin » Qua Jun 15, 2011 17:59
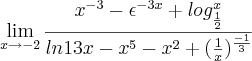
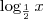Claudin escreveu:
Não consegui chegar a resolução do exercício.
Quem puder ajudar, favor postar a resolução.
Obrigado
por LuizAquino » Qui Jun 16, 2011 22:05
![\lim_{x\to 2} \frac{x^{-3}-e^{-3x}+\log_{\frac{1}{2}} x}{\ln 13x - x^5 - x^2 + \left(\frac{1}{x}\right)^{\frac{-1}{3}}} = \frac{2^{-3}-e^{-3\cdot 2}+\log_{\frac{1}{2}} 2}{\ln 13\cdot 2 - 2^5 - 2^2 + \left(\frac{1}{2}\right)^{\frac{-1}{3}}} = \frac{-\frac{7}{8} - e^{-6}}{\ln 26 - 36 + \sqrt[3]{2}}](/latexrender/pictures/c242bb0aaeaaf38c998958aa6f32b150.png "\lim_{x\to 2} \frac{x^{-3}-e^{-3x}+\log_{\frac{1}{2}} x}{\ln 13x - x^5 - x^2 + \left(\frac{1}{x}\right)^{\frac{-1}{3}}} = \frac{2^{-3}-e^{-3\cdot 2}+\log_{\frac{1}{2}} 2}{\ln 13\cdot 2 - 2^5 - 2^2 + \left(\frac{1}{2}\right)^{\frac{-1}{3}}} = \frac{-\frac{7}{8} - e^{-6}}{\ln 26 - 36 + \sqrt[3]{2}}")
por Claudin » Sáb Jun 18, 2011 02:33
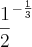
![\sqrt[3]{2}](/latexrender/pictures/9a132a1fa0d4f51451f00801ccbfe963.png "\sqrt[3]{2}")
![\sqrt[3]{\frac{1}{2}}](/latexrender/pictures/6e6f440da4aacca706144efe69411cc1.png "\sqrt[3]{\frac{1}{2}}")
por LuizAquino » Sáb Jun 18, 2011 11:39
Claudin escreveu:A resposta final seria essa?
por carlosalesouza » Seg Jun 20, 2011 11:01
Claudin escreveu:obs: E quando tinha
você colocou como equivalente
Achei que era
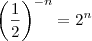, correto?![\left (\frac{1}{2}\right)^{-\frac{1}{3}}=2^\frac{1}{3}=\sqrt[3]{2}](/latexrender/pictures/dd5497fec7694f88f58303082ddcdb3c.png "\left (\frac{1}{2}\right)^{-\frac{1}{3}}=2^\frac{1}{3}=\sqrt[3]{2}")
, ok?por Claudin » Seg Jun 20, 2011 11:10
Voltar para Cálculo: Limites, Derivadas e Integrais
por Raphaela_sf » Qui Abr 05, 2012 19:26
Usuários navegando neste fórum: Nenhum usuário registrado e 4 visitantes
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png "\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}")
![\sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png "\sqrt[]{2}")
(dica : igualar a expressão a 
e elevar ao quadrado os dois lados)