 por Claudin » Sex Jun 03, 2011 15:31
por Claudin » Sex Jun 03, 2011 15:31
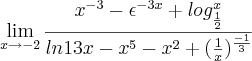
Não consegui chegar a resolução do exercício.
Quem puder ajudar, favor postar a resolução.
Obrigado
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por LuizAquino » Sex Jun 03, 2011 23:38
por LuizAquino » Sex Jun 03, 2011 23:38
Esse exercício está mal formulado.
Note, por exemplo, que temos a parcela
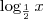
.
Além disso, o limite está sendo avaliado para x próximo de -2. Porém, sabemos que um logaritmando deve ser positivo e não nulo. Ou seja, devemos ter x > 0 naquela parcela.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Claudin » Seg Jun 06, 2011 17:08
por Claudin » Seg Jun 06, 2011 17:08
Confirmei na folha que eu retirei o exercício e era -2 mesmo, mas seria incoerente
Então deve ser +2
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Claudin » Qua Jun 15, 2011 17:59
por Claudin » Qua Jun 15, 2011 17:59
Claudin escreveu: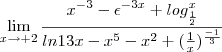
Não consegui chegar a resolução do exercício.
Quem puder ajudar, favor postar a resolução.
Obrigado
Alguém para responder o exercício com x tendendo a 2 positivo?
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Claudin » Sáb Jun 18, 2011 02:33
por Claudin » Sáb Jun 18, 2011 02:33
Até neste raciocínio eu cheguei.
A resposta final seria essa?
obs: E quando tinha
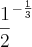
você colocou como equivalente
![\sqrt[3]{2} \sqrt[3]{2}](/latexrender/pictures/9a132a1fa0d4f51451f00801ccbfe963.png)
Achei que era
![\sqrt[3]{\frac{1}{2}} \sqrt[3]{\frac{1}{2}}](/latexrender/pictures/6e6f440da4aacca706144efe69411cc1.png)
Fica essa dúvida como observação!
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por LuizAquino » Sáb Jun 18, 2011 11:39
por LuizAquino » Sáb Jun 18, 2011 11:39
Claudin escreveu:A resposta final seria essa?
Sim.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por carlosalesouza » Seg Jun 20, 2011 11:01
por carlosalesouza » Seg Jun 20, 2011 11:01
Claudin escreveu:obs: E quando tinha
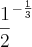
você colocou como equivalente
![\sqrt[3]{2} \sqrt[3]{2}](/latexrender/pictures/9a132a1fa0d4f51451f00801ccbfe963.png)
Achei que era
![\sqrt[3]{\frac{1}{2}} \sqrt[3]{\frac{1}{2}}](/latexrender/pictures/6e6f440da4aacca706144efe69411cc1.png)
Claudin, veja bem...
O expoente negativo inverte a fração, certo? Desse modo,
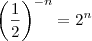
, correto?
Assim,
![\left (\frac{1}{2}\right)^{-\frac{1}{3}}=2^\frac{1}{3}=\sqrt[3]{2} \left (\frac{1}{2}\right)^{-\frac{1}{3}}=2^\frac{1}{3}=\sqrt[3]{2}](/latexrender/pictures/dd5497fec7694f88f58303082ddcdb3c.png)
, ok?
Um abraço
Carlos Alexandre
Ciências Contábeis - FECEA/PR
Matemática - UEPG/PR
-
carlosalesouza
- Colaborador Voluntário

-
- Mensagens: 103
- Registrado em: Sex Abr 29, 2011 17:28
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática -LIC
- Andamento: cursando
 por Claudin » Seg Jun 20, 2011 11:10
por Claudin » Seg Jun 20, 2011 11:10
Correto Carlos
Obrigado
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Limite] Gráfico e limite para função maior inteiro
 por Raphaela_sf » Qui Abr 05, 2012 19:26
por Raphaela_sf » Qui Abr 05, 2012 19:26
- 1 Respostas
- 6641 Exibições
- Última mensagem por LuizAquino

Qui Abr 05, 2012 20:53
Cálculo: Limites, Derivadas e Integrais
-
- [Limite] Limite de funções reais de várias variáveis
por Bianca_R » Dom Nov 04, 2012 17:17
- 1 Respostas
- 4786 Exibições
- Última mensagem por MarceloFantini

Dom Nov 04, 2012 19:37
Cálculo: Limites, Derivadas e Integrais
-
- [Limite trigonométrico] Como calculo este limite?
por Ronaldobb » Qua Nov 07, 2012 23:14
- 3 Respostas
- 5117 Exibições
- Última mensagem por Ronaldobb

Qui Nov 08, 2012 07:37
Cálculo: Limites, Derivadas e Integrais
-
- [Limite] limite trigonométrico quando x tende ao infinito
por Ge_dutra » Seg Jan 28, 2013 10:13
- 2 Respostas
- 7253 Exibições
- Última mensagem por Ge_dutra

Ter Jan 29, 2013 14:20
Cálculo: Limites, Derivadas e Integrais
-
- [Limite] Limite de funções piso (maior inteiro)
por ViniciusAlmeida » Sáb Fev 14, 2015 10:09
- 2 Respostas
- 4432 Exibições
- Última mensagem por adauto martins

Qui Fev 19, 2015 15:01
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
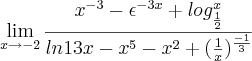

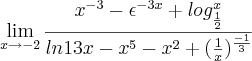

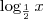 .
.


![\lim_{x\to 2} \frac{x^{-3}-e^{-3x}+\log_{\frac{1}{2}} x}{\ln 13x - x^5 - x^2 + \left(\frac{1}{x}\right)^{\frac{-1}{3}}} = \frac{2^{-3}-e^{-3\cdot 2}+\log_{\frac{1}{2}} 2}{\ln 13\cdot 2 - 2^5 - 2^2 + \left(\frac{1}{2}\right)^{\frac{-1}{3}}} = \frac{-\frac{7}{8} - e^{-6}}{\ln 26 - 36 + \sqrt[3]{2}} \lim_{x\to 2} \frac{x^{-3}-e^{-3x}+\log_{\frac{1}{2}} x}{\ln 13x - x^5 - x^2 + \left(\frac{1}{x}\right)^{\frac{-1}{3}}} = \frac{2^{-3}-e^{-3\cdot 2}+\log_{\frac{1}{2}} 2}{\ln 13\cdot 2 - 2^5 - 2^2 + \left(\frac{1}{2}\right)^{\frac{-1}{3}}} = \frac{-\frac{7}{8} - e^{-6}}{\ln 26 - 36 + \sqrt[3]{2}}](/latexrender/pictures/c242bb0aaeaaf38c998958aa6f32b150.png)

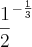
![\sqrt[3]{2} \sqrt[3]{2}](/latexrender/pictures/9a132a1fa0d4f51451f00801ccbfe963.png)
![\sqrt[3]{\frac{1}{2}} \sqrt[3]{\frac{1}{2}}](/latexrender/pictures/6e6f440da4aacca706144efe69411cc1.png)


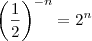 , correto?
, correto?![\left (\frac{1}{2}\right)^{-\frac{1}{3}}=2^\frac{1}{3}=\sqrt[3]{2} \left (\frac{1}{2}\right)^{-\frac{1}{3}}=2^\frac{1}{3}=\sqrt[3]{2}](/latexrender/pictures/dd5497fec7694f88f58303082ddcdb3c.png) , ok?
, ok?



 substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.